综合与实践
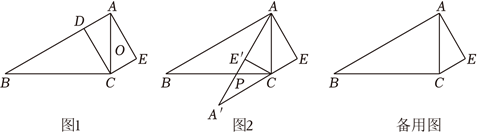
问题情境：如图（1）在 Rt $\triangle A B C$ 中，$\angle A C B=90^{\circ}, \angle B=30^{\circ}, A C=2, C D \perp A B$ 于点 $D$ ，点 $O$ 是 $A C$ 中点，将 $\triangle A D C$ 绕点 $O$ 旋转 $180^{\circ}$ 得到 $\triangle C E A$ ．

猜想证明：
（1）试判断四边形 $A D C E$ 的形状，并说明理由．
问题解决：
（2）将 $\triangle A E C$ 绕点 $C$ 逆时针方向旋转得到 $\triangle A^{\prime} E^{\prime} C$ ，当旋转到如图（2）位置时直线 $A^{\prime} E^{\prime}$ 刚好经过点 $A$ ．求证：$A^{\prime} C / / A B$ ，并求出此时 $\triangle A^{\prime} P C$ 的面积．
（3）在 $\triangle A E C$ 绕点 $C$ 旋转的过程中，直线 $A^{\prime} E^{\prime}$ 交 $A B$ 于点 $Q$ ，交 $B C$ 于点 $P$ ，是否存在某一时刻，使 $\triangle B P Q$ 是直角三角形．若存在，直接写出 $B P$ 的长，若不存在请说明理由．