如图所示,$M$ 是四面体 $O A B C$ 的棱 $B C$ 的中点,点 $N$ 在线段 $O M$ 上,点 $P$ 在线段 $A N$ 上,且 $A P=3 P N, \overrightarrow{O N}$ $=\frac{2}{3} \overrightarrow{O M}$ ,设 $\overrightarrow{O A}= a , \overrightarrow{O B}= b , \overrightarrow{O C}= c$ ,则下列等式成立的是( )
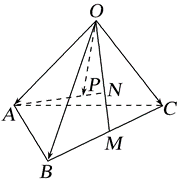
A
$\overrightarrow{O M}=\frac{1}{2} b-\frac{1}{2} c$
B
$\overrightarrow{A N}=\frac{1}{3} b+\frac{1}{3} c-a$
C
$\overrightarrow{A P}=\frac{1}{4} b-\frac{1}{4} c-\frac{3}{4} a$
D
$\overrightarrow{O P}=\frac{1}{4} a +\frac{1}{4} b +\frac{1}{4} c$
E
F