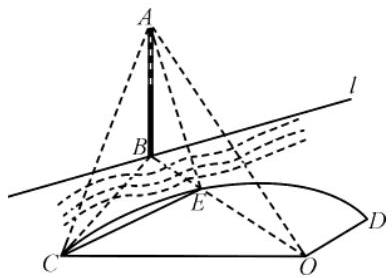
如图，有一段河流，河的一侧是以 $O$ 为圆心，半径为 $10 \sqrt{3} \mathrm{~m}$ 的扇形区域 $O C D$ ，河的另一侧是一段笔直的河岸 $l$ ，岸边有一烟囱 $A B$（不计 $B$ 离河岸的距离），且 $O B$ 的连线恰好与河岸 $l$ 垂直，设 $O B$ 与圆弧的交点为 $E$ ．经测量，扇形区域和河岸处于同一水平面，在点 $C$ ，点 $O$ 和点 $E$ 处测得烟囱 $A B$ 的仰角分别为 $45^{\circ}$ ， $30^{\circ}$ 和 $60^{\circ}$ 。
（1）求烟囱 $A B$ 的高度；
（2）如果要在 $C E$ 间修一条直路，求 $C E$ 的长．