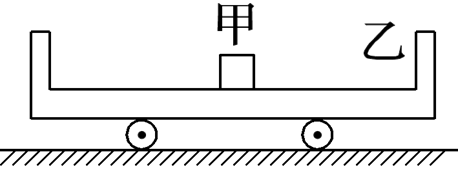
如图所示,两侧带有固定挡板的平板车乙静止在光滑水平地面上,挡板的厚度可忽略不计,车长为2L,与平板车质量相等的物块甲(可视为质点)由平板车的中点处以初速度v0向右运动,已知甲、乙之间的动摩擦因数为μ,重力加速度为g,忽略甲、乙碰撞过程中的能量损失,下列说法正确的是
A
甲、乙达到共同速度所需的时间为 $\frac{v_0}{2 \mu g}$
B
甲、乙共速前,乙的速度一定始终小于甲的速度
C
甲、乙相对滑动的总路程为 $\frac{v_0{ }^2}{4 \mu g}$
D
如果甲、乙碰撞的次数为 $n(n \neq 0)$ ,则最终甲距离乙左端的距离可能为 $\frac{v_0^2}{4 \mu g}+$ $L-2 n L$
E
F