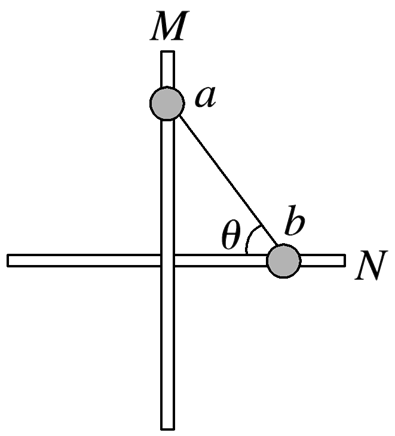
如图所示,竖直平面内固定两根足够长的细杆M、N,两杆无限接近但不接触,两杆间的距离可忽略不计.两个小球a、b(可视为质点)的质量相等,a球套在竖直杆M上,b球套在水平杆N上,a、b通过铰链用长度为L=0.5 m的刚性轻杆连接,将a球从图示位置由静止释放(轻杆与N杆的夹角为θ=53°),不计一切摩擦,已知
重力加速度的大小为g=10 m/s2,sin 53°=0.8,cos 53°
=0.6.在此后的运动过程中,下列说法正确的是
A
$a$ 球下落过程中,其加速度大小始终不大于 $g$
B
$a$ 球由静止下落 0.15 m 时,$a$ 球的速度大小为 $1.5 m / s$
C
$b$ 球的最大速度为 $3 \sqrt{2} m / s$
D
$a$ 球的最大速度为 $2 \sqrt{2} m / s$
E
F