如图为一种四颗星体组成的稳定系统,四颗质量均为m的星体位于边长为L的正方形四个顶点,四颗星体在同一平面内围绕同一点做匀速圆周运动,忽略其他星体对它们的作用,引力常量为G.下列说法中正确的是
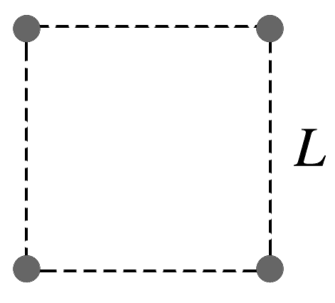
A
星体做匀速圆周运动的圆心不一定是正方形的中心
B
每颗星体做匀速圆周运动的角速度均为 $\sqrt{\frac{(4+\sqrt{2}) G m}{2 L^3}}$
C
若边长 $L$ 和星体质量 $m$ 均是原来的两倍,星体做匀速圆周运动的加速度大小是原来的两倍
D
若边长 $L$ 和星体质量 $m$ 均是原来的两倍,星体做匀速圆周运动的线速度大小不变
E
F