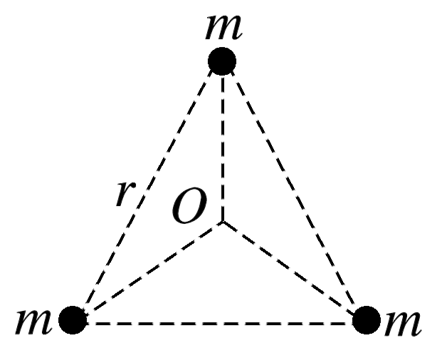
如图所示,质量相等的三颗星体组成三星系统,其他星体对它们的引力作用可忽略.设每颗星体的质量均为m,三颗星体分别位于边长为r的等边三角形的三个顶点上,它们绕某一共同的圆心O在三角形所在的平面内以相同的角速度做匀速圆周运动.已知引力常量为G,下列说法正确的是
A
每颗星体所需向心力大小为 $2 G \frac{m^2}{r^2}$
B
每颗星体运行的周期均为 $2 \pi \sqrt{\frac{r^3}{3 G m}}$
C
若 $r$ 不变,星体质量均变为 $2 m$ ,则星体的角速度变为原来的 $\sqrt{2}$ 倍
D
若 $m$ 不变,星体间的距离变为 $4 r$ ,则星体的线速度变为原来的 $\frac{1}{4}$
E
F