如图，在 $ A B C$ 中，$\angle C=90^{\circ}, \angle B=30^{\circ}, A C=3 cm, A D$ 是 $V A B C$ 的角平分线．动点 $P$ 从点 $A$ 出发，以 $\sqrt{3} cm / s$ 的速度沿折线 $A D-D B$ 向终点 $B$ 运动．过点 $P$ 作 $P Q / / A B$ ，交 $A C$ 于点 $Q$ ，以 $P Q$ 为边作等边三角形 $P Q E$ ，且点 $C, E$ 在 $P Q$ 同侧，设点 $P$ 的运动时间为 $t(s)(t>0)$ ， $V P Q E$ 与 $V A B C$重合部分图形的面积为 $S\left(cm^2\right)$ ．

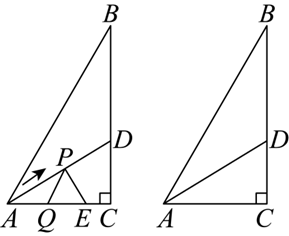
（1）当点 $P$ 在线段 $A D$ 上运动时，判断 $\triangle A P Q$ 的形状（不必证明），并直接写出 $A Q$ 的长（用含 $t$ 的代数式表示）。
（2）当点 $E$ 与点 $C$ 重合时，求 $t$ 的值．
（3）求 $S$ 关于 $t$ 的函数解析式，并写出自变量 $t$ 的取值范围．