已知抛物线 $y=-x^2+b x+c$ 与 $x$ 轴交于点 $A(-1,0), B(3,0)$ ．

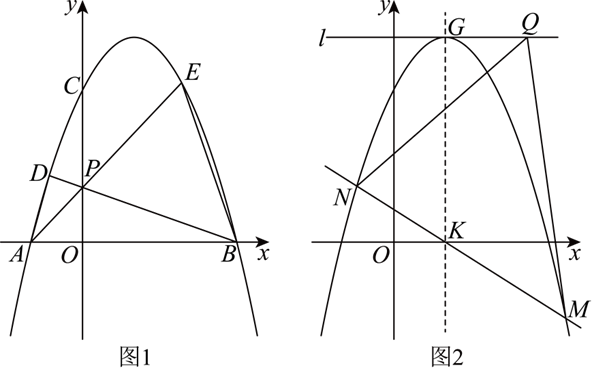
（1）求抛物线的解析式；
（2）如图1，抛物线与 $y$ 轴交于点 $C$ ，点 $P$ 为线段 $O C$ 上一点（不与端点重合），直线 $P A, P B$ 分别交抛物线于点 $E, D$ ，设 $V P A D$ 面积为 $S_1, \triangle P B E$ 面积为 $S_2$ ，求 $\frac{S_1}{S_2}$ 的值；
（3）如图2，点 $K$ 是抛物线对称轴与 $x$ 轴的交点，过点 $K$ 的直线（不与对称轴重合）与抛物线交于点 $M, N$ ，过抛物线顶点 $G$ 作直线 $l / / x$ 轴，点 $Q$ 是直线 $l$ 上一动点．求 $Q M+Q N$ 的最小值．