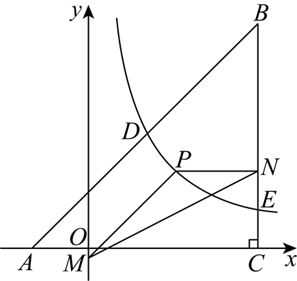
如图， $\triangle A B C$ 中，$A C=B C, \angle A C B=90^{\circ}, A(-2,0), C(6,0)$ ，反比例函数 $y=\frac{k}{x}(k \neq 0, x>0)$ 的图象与 $A B$交于点 $D(m, 4)$ ，与 $B C$ 交于点 $E$ ．
（1）求 $m, k$ 的值；
（2）点 $P$ 为反比例函数 $y=\frac{k}{x}(k \neq 0, x>0)$ 图象上一动点（点 $P$ 在 $D, E$ 之间运动，不与 $D, E$ 重合），过点 $P$作 $P M / / A B$ ，交 $y$ 轴于点 $M$ ，过点 $P$ 作 $P N / / x$ 轴，交 $B C$ 于点 $N$ ，连接 $M N$ ，求 $V P M N$ 面积的最大值，并求出此时点 $P$ 的坐标．