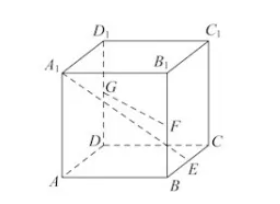
在棱长为 4 的正方体 $A B C D - A _1 B _1 C _{ 1 } D _1$ 中, $E , F , G$ 分别是棱 $B C , B B_{ b } D D_1$ 的中点,过 $F G$ 作平面 $\alpha$ ,使得 $A _{ 1 } E / / \alpha$ ,则点 A 到平面 $\alpha$ 的距离是
A
$\frac{2 \sqrt{17}}{17}$
B
$\frac{6 \sqrt{17}}{17}$
C
$\frac{10 \sqrt{17}}{17}$
D
$\frac{14 \sqrt{17}}{17}$
E
F