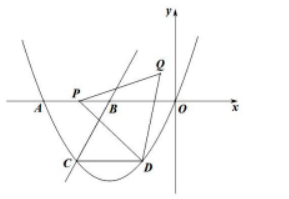
如图, 已知抛物线 $y=a x^2+\frac{4 \sqrt{3}}{3} x+c(a \neq 0)$ 经过原 点 $O$, 与 $x$ 轴交于点 $A(-4 \sqrt{3}, 0)$, 直线 $y=\sqrt{3} x+6$ 交
（1）求抛物线的解析式:
(2)若点 $D$ 是点 $C$ 关于抛物线对称轴的对称点, 连接 $C D$, 求 $C D$ 的长;
(3) 若点 $P$ 为线段 $A O$ 上的一个动点, 连接 $P D$, 以 $P D$ 为边向右作等边三角形 $P D Q$. 当点 $P$ 从点 $A$ 开始向右运动到点 $O$ 时, 线段 $D Q$ 扫过的面积为