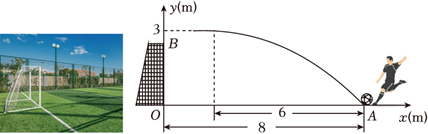
一次足球训练中, 小明从球门正前方 $8 m$ 的 $A$ 处射门, 球射向球门的路线呈抛物线. 当球飞行的水平距离为 $6 m$ 时, 球达到最高点, 此时球离地面 $3 m$. 已知球门高 $O B$ 为 $2.44 m$, 现以 $O$ 为原点建立如图所示直角坐标系.
(1)求抛物线的函数表达式, 并通过计算判断球能否射进球门(忽略其他因素);
(2) 对本次训练进行分析, 若射门路线的形状、最大高度均保持不变, 则当时他应该带球向正后方移动多少米射门, 才能让足球经过点 $O$ 正上方 2.25 m 处?