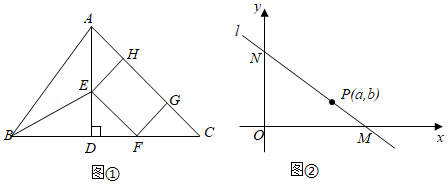
如图(1), 在 $\triangle A B C$ 中, $A D \perp B C$ 于点 $D, B C=14, A D=8, B D=6$, 点 $E$ 是 $A D$ 上一动点 (不 与点 $A, D$ 重合), 在 $\triangle A D C$ 内作矩形 $E F G H$, 点 $F$ 在 $D C$ 上, 点 $G, H$ 在 $A C$ 上, 设 $D E$ $=x$, 连接 $B E$.
(1) 当矩形 $E F G H$ 是正方形时, 直接写出 $E F$ 的长;
(2) 设 $\triangle A B E$ 的面积为 $S_{1}$, 矩形 $E F G H$ 的面积为 $S_{2}$, 令 $y=\frac{S_{1}}{S_{2}}$, 求 $y$ 关于 $x$ 的函数解析 式(不要求写出自变量 $x$ 的取值范围);
(3) 如图(2), 点 $P(a, b)$ 是 (2) 中得到的函数图象上的任意一点, 过点 $P$ 的直线 $l$ 分 别与 $x$ 轴正半轴, $y$ 轴正半轴交于 $M, N$ 两点, 求 $\triangle O M N$ 面积的最小值, 并说明理由.