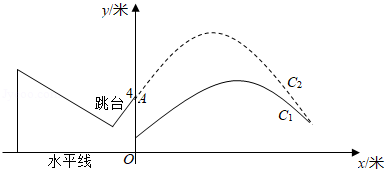
2022 年北京冬奥会即将召开, 激起了人们对冰雪运动的极大热情. 如图是某跳台滑雪训 练场的横截面示意图, 取某一位置的水平线为 $x$ 轴, 过跳台终点 $A$ 作水平线的垂线为 $y$ 轴, 建立平面直角坐标系, 图中的抛物线 $C_{1}: y=-\frac{1}{12} x^{2}+\frac{7}{6} x+1$ 近似表示滑雪场地上的一 座小山坡, 某运动员从点 $O$ 正上方 4 米处的 $A$ 点滑出, 滑出后沿一段抛物线 $C_{2}: y=$ $-\frac{1}{8} x^{2}+b x+c$ 运动.
(1) 当运动员运动到离 $A$ 处的水平距离为 4 米时, 离水平线的高度为 8 米, 求抛物线 $C_{2}$ 的函数解析式 (不要求写出自变量 $x$ 的取值范围);
(2) 在 (1) 的条件下, 当运动员运动的水平距离为多少米时, 运动员与小山坡的坚直距 离为 1 米?
(3) 当运动员运动到坡顶正上方, 且与坡顶距离超过 3 米时, 求 $b$ 的取值范围.