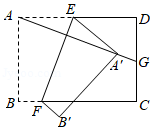
如图, 矩形纸片 $A B C D, A D: A B=\sqrt{2}: 1$, 点 $E, F$ 分别在 $A D, B C$ 上, 把纸片如图沿 $E F$ 折叠, 点 $A, B$ 的对应点分别为 $A^{\prime}, B^{\prime}$, 连接 $A A^{\prime}$ 并延长交线 段 $C D$ 于点 $G$, 则 $\frac{E F}{A G}$ 的值为()
A
$\frac{\sqrt{2}}{2}$
B
$\frac{2}{3}$
C
$\frac{1}{2}$
D
$\frac{\sqrt{5}}{3}$
E
F