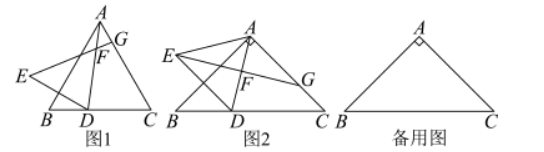
在 $\triangle A B C$ 中， $A B=A C$ ，点 $D$ 是 $B C$ 边上一点（点 $D$ 不与端点重合）. 点 $D$ 关于直线 $A B$ 的对称点为点 $E$ ，连接 $A D, D E$. 在直线 $A D$ 上取一点 $F$ ，使 $\angle E F D=\angle B A C$ ，直线 $E F$ 与直线 $A C$ 交于点 $G$.
(1)如图1，若 $\angle B A C=60^{\circ}, B D < C D, \angle B A D=\alpha$ ，求 $\angle A G E$ 的度数（用含 $\alpha$ 的代数式表示）；
(2)如图1，若 $\angle B A C=60^{\circ}, B D < C D$ ，用等式表示线段 $C G$ 与 $D E$ 之间的数量关系，并证明；
(3)如图2，若 $\angle B A C=90^{\circ}$ ，点 $D$ 从点 $B$ 移动到点 $C$ 的过程中，连接 $A E$ ，当 $\triangle A E G$ 为等腰二角形时，请直接写出此时 $\frac{C G}{A G}$ 的值.