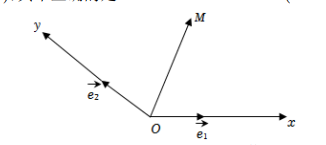
如图所示, 设 $O x, O y$ 是平面内相交成 $\theta\left(\theta \neq \frac{\pi}{2}\right)$ 角的两条数轴, $\overrightarrow{\mathrm{e}}_1, \overrightarrow{\mathrm{e}}_2$ 分别是与 $x$ 轴, $y$ 轴正方向同向的单位向量, 则称平面坐标系 $x O y$ 为 $\theta$ 反射坐标系. 在 $\theta$ 反射坐标系中, 若 $\overrightarrow{O M}=x \overrightarrow{\mathrm{e}_1}+y \overrightarrow{\mathrm{e}_2}$, 则把有序数对 $(x, y)$ 称为向量 $\overrightarrow{O M}$ 的反射坐标, 记为 $\overrightarrow{O M}=(x, y)$. 在 $\theta=\frac{2 \pi}{3}$ 的反射坐标系中, $\vec{a}=(1,2), \vec{b}=(2,-1)$, 其中正确的是
A
$\vec{a}-\vec{b}=(-1,3)$
B
$|\vec{a}|=\sqrt{5}$
C
$\vec{a} \perp \vec{b}$
D
$|\vec{b}|=\sqrt{7}$
E
F