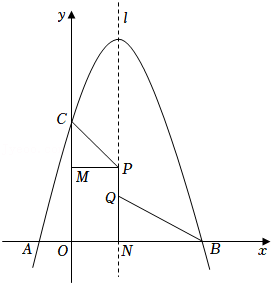
如图, 抛物线 $y=-x^{2}+3 x+4$ 与 $x$ 轴交于 $A, B$ 两点 (点 $A$ 位于点 $B$ 的左侧), 与 $y$ 轴交于 $C$ 点, 抛物线的对称轴 $l$ 与 $x$ 轴交于点 $N$, 长为 1 的线段 $P Q$ (点 $P$ 位于点 $Q$ 的上 方) 在 $x$ 轴上方的抛物线对称轴上运动.
(1) 直接写出 $A, B, C$ 三点的坐标;
(2) 求 $C P+P Q+Q B$ 的最小值;
(3) 过点 $P$ 作 $P M \perp y$ 轴于点 $M$, 当 $\triangle C P M$ 和 $\triangle Q B N$ 相似时, 求点 $Q$ 的坐标.