科数网
题号:12154 题型:解答题 来源:安徽淮南凤台县八年级初中数学竞赛
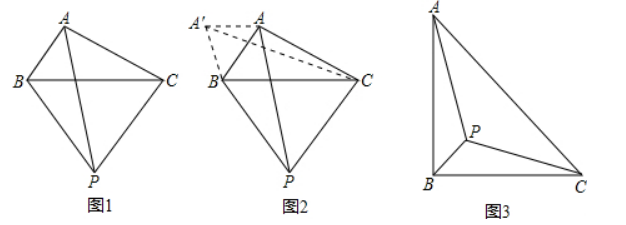
小伟遇到这样一个问题: 如图 1, 在
△
A
B
C
(其中
∠
B
A
C
是一个可以变化的角) 中,
A
B
=
2
,
A
C
=
4
, 以
B
C
为边在
B
C
的下方作等边
△
P
B
C
, 求
A
P
的最大值.
小伟是这样思考的: 利用变换和等边三角形将边的位置重新组合. 他的方法是以点
B
为旋转中心将
△
A
B
P
逆时针旋转
60
∘
得到
△
A
′
B
C
, 连接
A
′
A
, 当点
A
落在
A
′
C
上时, 此题可解 (如图2).
请你回答:
A
P
的最大值是
参考小伟同学思考问题的方法, 解决下列问题:
如图3, 等腰Rt
△
A
B
C
. 边
A
B
=
4
,
P
为
△
A
B
C
内部一点, 则
A
P
+
B
P
+
C
P
的最小值是 . ( 结果可以不化简)
A.
B.
C.
D.
0 人点赞
124 次查看
白板
加入试卷
答案：
解析：
答案与解析：
答案仅限会员可见
微信内自动登录
或
手机登录
或
微信扫码注册登录
点击我要
开通VIP
