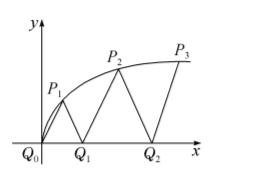
如图, 曲线 $y=\sqrt{x}$ 下有一系列等边三角形, 设第 $n$ 个等边三角形 $Q_{n-1} P_n Q_n\left(Q_0\right.$ 为坐标原点) 的边长为 $a_n$, 则下列说法正确的有
A
$a_1=\frac{2}{3}, a_2=\frac{4}{3}$
B
记 $S_n$ 为数列 $\left\{a_n\right\}$ 的前 $n$ 项和, 则 $P_{n+1}$ 为 $\left(S_n+\frac{a_{n+1}}{2}, \frac{\sqrt{3}}{2} a_{n+1}\right)$
C
记 $S_n$ 为数列 $\left\{a_n\right\}$ 的前 $n$ 项和, 则 $S_n=\frac{3}{4} a_{n+1}^2+\frac{1}{2} a_{n+1}$
D
数列 $\left\{a_n\right\}$ 的通项公式为 $a_n=\frac{2 n}{3}$
E
F