一、单选题 （共 7 题，每小题 5 分，共 50 分，每题只有一个选项正确）
一质点在平面上运动, 已知质点位置矢量的表示式为 $\vec{r}=a t^2 \vec{i}+b t^2 \vec{j}$ (其中 $a 、 b$ 为常量), 则该质点作
$\text{A.}$ 匀速直线运动.
$\text{B.}$ 变速直线运动.
$\text{C.}$ 抛物线运动.
$\text{D.}$ 一般曲线运动.
一平面简谐波的表达式为 $y=0.1 \cos (3 \pi t-\pi x+\pi)(\mathrm{SI}), t=0$ 时的波形曲线如图所示，则
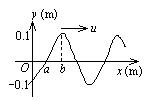
$\text{A.}$ $O$ 点的振幅为 $-0.1 \mathrm{~m}$
$\text{B.}$ 波长为 $3 \mathrm{~m}$
$\text{C.}$ $a 、 b$ 两点间相位差为 $\frac{1}{2} \pi$
$\text{D.}$ 波速为 $9 \mathrm{~m} / \mathrm{s}$
图为沿 $x$ 轴负方向传播的平面简谐波在 $t=0$ 时刻的波形. 若波的表达式以余弦函数表示, 则 $O$ 点处质点振动的初相为
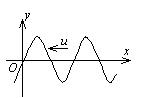
$\text{A.}$ 0
$\text{B.}$ $\frac{1}{2} \pi$
$\text{C.}$ $\pi$
$\text{D.}$ $\frac{3}{2} \pi$
关于温度的意义, 下列几种说法中错误的是
$\text{A.}$ 气体的温度是分子平动动能的量度;
$\text{B.}$ 气体的温度是大量气体分子热运动的集体表现, 具有统计意义;
$\text{C.}$ 温度的高低反映物质内部分子运动剧烈程度的不同;
$\text{D.}$ 从微观上看, 气体的温度表示每个气体分子的冷热程度。
气缸内盛有一定量的氢气 (可视作理想气体), 当温度不变而压强增大一倍时, 氢气分子的平均碰撞次数 $\bar{Z}$ 和平均自由程 $\bar{\lambda}$ 的变化情况是
$\text{A.}$ $\bar{Z}$ 和 $\bar{\lambda}$ 都增大一倍;
$\text{B.}$ $\bar{Z}$ 和 $\bar{\lambda}$ 都减为原来的一半;
$\text{C.}$ $\bar{Z}$ 增大一倍而 $\bar{\lambda}$ 减为原来的一半;
$\text{D.}$ $\bar{Z}$ 减为原来的一半陑 $\bar{\lambda}$ 增大一倍。
一卡诺热机的高温热源和低温热源温度分别为 $527^{\circ} \mathrm{C}$ 和 $227^{\circ} \mathrm{C}$, 热机在最大 效率下工作, 每一循环吸热 $1600 \mathrm{~J}$, 此热机每一循环对外做功
$\text{A.}$ $200 \mathrm{~J}$;
$\text{B.}$ $300 \mathrm{~J}$;
$\text{C.}$ $400 \mathrm{~J}$;
$\text{D.}$ $600 \mathrm{~J}$;
在某地发生两件事, 静止位于该地的甲测得时间间隔为 $4 \mathrm{~s}$, 若相对于甲作匀速直线运 动的乙测得时间间隔为 $5 \mathrm{~s}$, 则乙相对于甲的运动速度是 $(c$ 表示真空中光速)
$\text{A.}$ $(4 / 5) \mathrm{c}$.
$\text{B.}$ $(3 / 5) \mathrm{c}$.
$\text{C.}$ $(2 / 5) c$.
$\text{D.}$ $(1 / 5) \mathrm{c}$.
二、填空题 （共 2 题, 每小题 5 分，共 20 分， 请把答案直接填写在答题纸上）
一个质点作半径为 $\mathrm{R}$ 的圆周运动, 角运动方程为 $\theta=4+5 t^2$, 则质点运动的切向加速度为
热力学第二定律的表明一切与热现象相关的实际过程都是 （填写可逆或不可逆）。
三、解答题 （ 共 7 题，满分 80 分，解答过程应写出必要的文字说明、证明过程或演算步骤 ）
一轻绳跨过两个质量均为 $\mathrm{m}$, 半径均 为 $\mathrm{r}$ 的均匀圆盘状定滑轮,绳的两端分别挂着质量 分别为 $\mathrm{m}$ 和 $2 \mathrm{~m}$ 的重物, 如图所示,绳与滑轮间无相 对滑动,滑轮轴光滑,两个定滑轮的转动惯量均为 $\mathrm{mr}^2 / 2$. 将由两个定滑轮以及质量为 $\mathrm{m}$ 和 $2 \mathrm{~m}$ 的重物 组成的系统从静止释放, 求三段绳内的张力
一飞轮边缘上一点所经过的路程与时间的关系为 $s=v_0 t-\frac{1}{2} b t^2, v_0 、 b$ 都是正的常量.
(1) 求该点在时刻 $t$ 的加速度. (2) $t$ 为何值时, 该点的切向加速度与法向加速度的大小 相等? 已知飞轮的半径为 $R$.
一轻绳跨过一定滑轮, 滑轮视为圆盘, 绳的两端分别悬有质量为 $m_1$ 和 $m_2$ 的物体 1 和 $2, m_1 < m_2$, 如图 3-9 所示. 设滑轮的质量为 $m$, 半径为 $r$. 绳与滑轮之间无相对滑动, 且滑 轮轴处的摩擦可忽略不计. 试求物体的加速度和绳的张力.
一平面简谐波沿 $x$ 轴正向传播，其振幅和角频率分别为 $A$ 和 $\omega$, 波速为 $u$, 设 $t=0$ 时的波形曲线如图所示.
(1)写出此波的表达式.
(2)求距 $O$ 点分别为 $\lambda / 8$ 和 $3 \lambda / 8$ 两处质点的振动方程.
(3)求距 $O$ 点分别为 $\lambda / 8$ 和 $3 \lambda / 8$ 两处质点在 $t=0$ 时的振动速度.
有 $3.2 \times 10^{-2} \mathrm{~kg}$ 氧气作 $\mathrm{ABCDA}$ 循环过程, 加图 5 所示, $\mathrm{A} \rightarrow \mathrm{B}$ 和 $\mathrm{C} \rightarrow \mathrm{D}$ 都为等温过程, 设 $T_1=300 \mathrm{~K}, \mathrm{~T}_2=200 \mathrm{~K}, \mathrm{~V}_2=2 \mathrm{~V}_1$ 。 求 (1) $\mathrm{A} \rightarrow \mathrm{B} 、 \mathrm{~B}$ $\rightarrow \mathrm{C} 、 \mathrm{C} \rightarrow \mathrm{D} 、 \mathrm{D} \rightarrow \mathrm{A}$ 各个过程系统吸收的热量 ; (2) 系统完成一次循环所作的净 功; (3) 此循环的效率。
一容器储有多原子分子气体, 可视为理想气体, 该气体分子质量 $\mathrm{m}=3.0 \times 10^{-26} \mathrm{~kg}$, 其压强为一个标准大气压, 温度为 $t=27^{\circ} \mathrm{C}$ 。求: (1) 该气体分子 的方均根速率; (2) 该气体的质量密度 $\rho$; (3) 该气体分子的平均动能。
在惯性系 $S$ 中, 两事件发生在同一地点而时间相隔为 8 秒, 另一惯性系 $S^{\prime}$ 以速度 $v=0.6 c$ 相对于 $S$ 运动, 则 $S^{\prime}$ 系中测得的两事件的空间间隔是多少?