解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
甲、乙两门高射炮彼此独立地向一架飞机各发一炮, 甲、乙击中飞机的概率分别为 0.3 和 0.4 , 则飞机至少被击中一炮的概率为?
设随机变量 $A$ 为 $x \in(-5,7)$ 上的均匀分布, 则关于 $x$ 的方程 $9 x^2+6 A x+A+6=0$ 有实根的概率为?
仓库中有 10 箱同种规格的产品, 其中 2 箱、 3 箱、 5 箱分别由甲、乙、丙三个厂生产, 三个厂的正品率分别为 $0.7,0.8,0.9$, 现在从这 10 箱产品中任取一箱, 再从中任取一件
(1) 求取出的产品为正品的概率
(2) 如果取出的是正品, 求此件产品由乙厂生产的概率
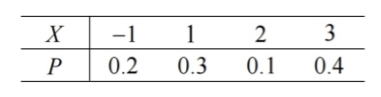
设随机变量 $X$ 的分布律如下: 求: (1) $X$ 的分布函数; (2) $ P\{1 \leq X < 3\} $
设随机变量 $X$ 的概率密度为 $f(x)= \begin{cases}x & 0 \leq x < 1 \\ 2-x & 1 \leq x < 2 \\ 0 & \text { 其他 }\end{cases}$
求: (1) $X$ 的分布函数 $F(x)$
(2) 求 $P\left\{1 < X < \frac{3}{2}\right\}$
设随机变量 $X$ 的概率密度为 $f(x)=\left\{\begin{array}{ll}\frac{x}{2} & 0 < x < A \\ 0 & \text { 其他 }\end{array}\right.$, 求:
(1) 常数 $A$
(2) 分布函数 $F(x)$
(3) $P\left\{-1 < X < \frac{1}{2}\right\}$