单选题 (共 6 题 ),每题只有一个选项正确
一质量为m的乘客乘坐竖直电梯下楼,其位移s与时间t的关系图像如图所示.乘客所受支持力的大小用FN表示,速度大小用v表示.重力加速度大小为g.以下判断正确的是
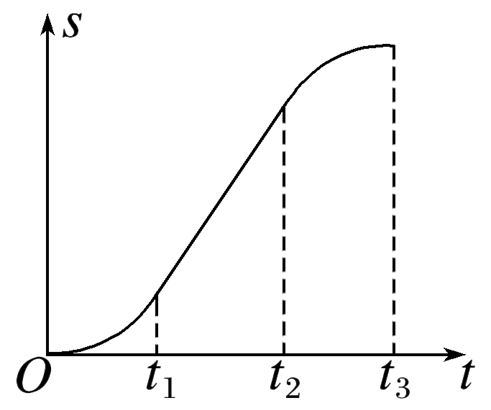
$\text{A.}$ 0~t1时间内,v增大,FN>mg
$\text{B.}$ t1~t2 时间内,v减小,FN < mg
$\text{C.}$ t2~t3 时间内,v增大,FN < mg
$\text{D.}$ t2~t3时间内,v减小,FN>mg
水平路面上质量为30 kg的小车,在60 N水平推力作用下由静止开始以1.5 m/s2的加速度做匀加速直线运动.2 s后撤去该推力,则下列说法正确的是
$\text{A.}$ 小车2 s末的速度大小是4 m/s
$\text{B.}$ 小车受到的阻力大小是15 N
$\text{C.}$ 撤去推力后小车的加速度大小是1 m/s2
$\text{D.}$ 小车运动的总时间为6 s
如图所示,一根弹簧一端固定在左侧竖直墙上,另一端连着A小球,同时水平细线一端连着A球,另一端固定在右侧竖直墙上,弹簧与竖直方向的夹角是60°,A、B两小球分别连在另一根竖直弹簧两端.开始时A、B两球都静止不动,A、B两小球的质量相等,重力加速度为g,若不计弹簧质量,在水平细线被剪断瞬间,A、B两球的加速度大小分别为
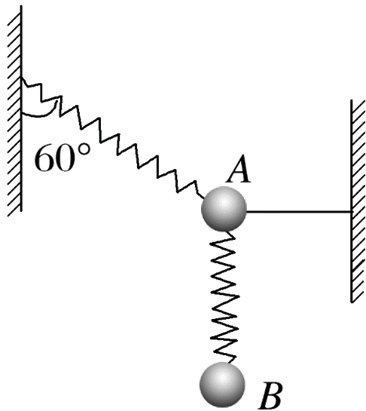
$\text{A.}$ $a_A=a_B=g$
$\text{B.}$ $a_A=2 g, a_B=0$
$\text{C.}$ $a_A=\sqrt{3} g, \quad a_B=0$
$\text{D.}$ $a_A=2 \sqrt{3} g, \quad a_B=0$
如图所示,有一半圆,其直径水平且与另一圆的底部相切于O点,O点恰好是下半圆的圆心,它们处在同一竖直平面内.现有三条光滑直轨道AOB、COD、EOF,它们的两端分别位于上下两圆的圆周上,轨道与竖直直径的夹角关系为α > β > θ.现让一小物块先后从三条轨道顶端由静止下滑至底端,则小物块在每一条倾斜轨道上滑动时所经历的时间关系为

$\text{A.}$ $t_{A B}=t_{C D}=t_{E F}$
$\text{B.}$ $t_{A B}>t_{C D}>t_{E F}$
$\text{C.}$ $t_{A B} < t_{C D} < t_{E F}$
$\text{D.}$ $t_{A B}=t_{C D} < t_{E F}$
如图所示,在竖直平面内有半径为R和2R的两个圆,两圆的最高点相切,切点为A.B和C分别是小圆和大圆上的两个点,其中AB长为 ,AC长为 .现沿AB和AC建立两条光滑轨道,自A处由静止释放小球(可看为质点),已知小球沿AB轨道运动到B点所用时间为t1,沿AC轨道运动到C点所用时间为t2,则t1与t2之比为

$\text{A.}$ $1: 3$
$\text{B.}$ $1: 2$
$\text{C.}$ $1: \sqrt{3}$
$\text{D.}$ $1: \sqrt{2}$
如图所示,A、B、C为三个实心小球,A为铁球,B、C为木球.A、B两球分别连接在两根弹簧上,C球连接在细线一端,弹簧和细线的下端固定在装水的杯子底部,该水杯置于用绳子悬挂的静止吊篮内.若将挂吊篮的绳子剪断,则剪断的瞬间相对于杯底(不计空气阻力,ρ木 < ρ水 < ρ铁)

$\text{A.}$ A球将向上运动,B、C球将向下运动
$\text{B.}$ A、B球将向上运动,C球不动
$\text{C.}$ A球将向下运动,B球将向上运动,C球不动
$\text{D.}$ A球将向上运动,B球将向下运动,C球不动
多选题 (共 3 题 ),每题有多个选项正确
一人乘电梯上楼,在竖直上升过程中加速度a随时间t变化的图线如图所示,以竖直向上为a的正方向,则人对地板的压力

$\text{A.}$ t=2 s时最大
$\text{B.}$ t=2 s时最小
$\text{C.}$ t=8.5 s时最大
$\text{D.}$ t=8.5 s时最小
如图所示,光滑斜面CA、DA、EA都以AB为底边,三个斜面的倾角分别为75°、45°、30°.物体分别沿三个斜面从顶端由静止滑到底端,下列说法中正确的是

$\text{A.}$ 物体沿CA下滑,加速度最大
$\text{B.}$ 物体沿EA下滑,加速度最大
$\text{C.}$ 物体沿CA滑到底端所需时间最短
$\text{D.}$ 物体沿DA滑到底端所需时间最短
奥运冠军全红婵在第14届全运会上再次上演“水花消失术”夺冠.在女子10 m跳台的决赛中(下面研究过程将全红婵视为质点),全红婵竖直向上跳离跳台的速度为5 m/s,竖直入水后到速度减为零的运动时间与空中运动时间相等,假设所受水的阻力恒定,不计空气阻力,全红婵的体重为35 kg,重力加速度大小取g=10 m/s2,则
$\text{A.}$ 跳离跳台后上升阶段全红婵处于失重状态
$\text{B.}$ 入水后全红婵处于失重状态
$\text{C.}$ 全红婵在空中运动的时间为1.5 s
$\text{D.}$ 入水后全红婵受到水的阻力为612.5 N
解答题 (共 2 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
物流公司通过滑轨把货物直接装运到卡车中,如图所示,倾斜滑轨与水平面成24°角,长度l1=4 m,水平滑轨长度可调,两滑轨间平滑连接.若货物从倾斜滑轨顶端由静止开始下滑,其与滑轨间的动摩擦因数均为μ= ,货物可视为质点(取cos 24°=0.9,sin 24°=0.4,重力加速度g=10 m/s2).

(1)求货物在倾斜滑轨上滑行时加速度a1的大小;
(2)求货物在倾斜滑轨末端时速度v的大小;
(3)若货物滑离水平滑轨末端时的速度不超过2 m/s,求水平滑轨的最短长度l2.
某航母上舰载机起飞时主要靠甲板前端上翘来帮助战斗机起飞,其示意图如图所示,飞机由静止开始先在一段水平距离为 $L_1=160 m$ 的水平跑道上运动,然后在长度为 $L_2=20.5 m$ 的倾斜跑道上滑跑,直到起飞.已知飞机的质量 $m=2.0 \times 10^4 kg$ ,其喷气发动机的推力大小恒为 $F=1.4 \times 10^5 N$ ,方向与速度方向相同,水平跑道与倾斜跑道末端的高度差 $h=2.05 m$ ,飞机在水平跑道上和倾斜跑道上运动的过程中受到的平均阻力大小都为飞机重力的 0.2 倍,假设航母处于静止状态,飞机质量视为不变并可看成质点,倾斜跑道看作斜面,不计水平跑道和倾斜跑道连接处的影响,且飞机起飞的过程中没有出现任何故障,取 $g=10 m / s ^2$ .求:
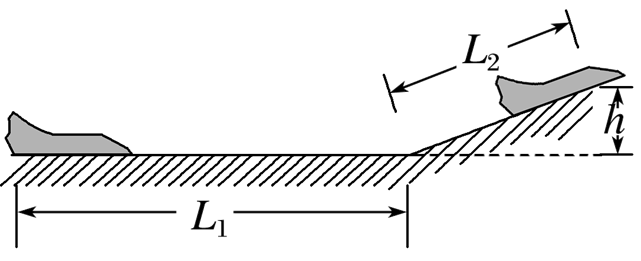
(1)飞机在水平跑道上运动的末速度大小;
(2)飞机从开始运动到起飞经历的时间t.