单选题 (共 4 题 ),每题只有一个选项正确
阅读以下作图步骤:
(1)在 $O A$ 和 $O B$ 上分别截取 $O C, O D$, 使 $O C=O D$;
(2)分别以 $C, D$ 为圆心, 以大于 $\frac{1}{2} C D$ 的长为半径作弧, 两弧在 $\angle A O B$ 内交于点 $M$;
(3)作射线 $O M$, 连接 $C M, D M$, 如图所示.
根据以上作图, 一定可以推得的结论是

$\text{A.}$ $\angle 1=\angle 2$ 且 $C M=D M$
$\text{B.}$ $\angle 1=\angle 3$ 且 $C M=D M$
$\text{C.}$ $\angle 1=\angle 2$ 且 $O D=D M$
$\text{D.}$ $\angle 2=\angle 3$ 且 $O D=D M$
为贯彻落实教育部办公厅关于“保障学生每天校内、校外各1小时体育活动时间”的要求,学校要求学生每天坚持体育锻炼.小亮记录了自己一周内每天校外锻炼的时间(单位:分钟),并制作了如图所示的统计图.根据统计图,下列关于小亮该周每天校外锻炼时间的描述,正确的是

$\text{A.}$ 平均数为70分钟
$\text{B.}$ 众数为67分钟
$\text{C.}$ 中位数为67分钟
$\text{D.}$ 方差为0
如图, 正方形四个顶点分别位于两个反比例函数 $y=\frac{3}{{x}}$ 和 $y=\frac{{n}}{{x}}$ 的图象的四个分支上, 则实数 $n$ 的值为

$\text{A.}$ -3
$\text{B.}$ $-\frac{1}{3}$
$\text{C.}$ $\frac{1}{3}$
$\text{D.}$ 3
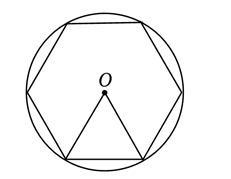
我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的 “割圆术”, 即利用圆的内接正多边形逼近圆的方法来近似估算, 指出 “割之弥细, 所失弥少. 割之又割,以至于不可割, 则与圆周合体, 而无所失矣”. “割圆术” 孕育了微积分思想, 他用这种思想得到了圆周率 $\pi$ 的近似值为 3.1416. 如图, $\odot O$ 的半径为 1 , 运用 “割圆术”, 以圆内接正六边形面积近似估计 $\odot O$ 的面积, 可得 $\pi$ 的估计值为 $\frac{3 \sqrt{3}}{2}$, 若用圆内接正十二边形作近似估计, 可得 $\pi$ 的估计值为
$\text{A.}$ $\sqrt{3}$
$\text{B.}$ $2 \sqrt{2}$
$\text{C.}$ 3
$\text{D.}$ $2 \sqrt{3}$
填空题 (共 1 题 ),请把答案直接填写在答题纸上
已知抛物线 $y=a x^2-2 a x+b(a>0)$ 经过 $A\left(2 n+3, y_1\right), B\left(n-1, y_2\right)$ 两点,若 $A, B$ 分别位于抛物线对称轴的两侧, 且 $y_1 < y_2$, 则 $n$ 的取值范围是
解答题 (共 2 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知抛物线 $y=a x^2+b x+3$ 交 $x$ 轴于 $A(1,0), B(3,0)$ 两点, $M$ 为抛物线的顶点, $C, D$为抛物线上不与 $A, B$ 重合的相异两点, 记 $A B$ 中点为 $E$, 直线 $A D, B C$ 的交点为 $P$.
(1)求抛物线的函数表达式;
(2)若 $C(4,3), D\left(m,-\frac{3}{4}\right)$, 且 $m < 2$, 求证: $C, D, E$ 三点共线;
(3)小明研究发现: 无论 $C, D$ 在抛物线上如何运动, 只要 $C, D, E$ 三点共线, $\triangle A M P$, $\triangle M E P, \triangle A B P$ 中必存在面积为定值的三角形. 请直接写出其中面积为定值的三角形及其面积, 不必说明理由.
如图 1, 在 $\triangle A B C$ 中, $\angle B A C=90^{\circ}, A B=A C, D$ 是 $A B$ 边上不与 $A, B$ 重合的一个定点. $A O \perp B C$ 于点 $O$, 交 $C D$ 于点 $E . D F$ 是由线段 $D C$ 绕点 $D$ 顺时针旋转 $90^{\circ}$得到的, $F D, C A$ 的延长线相交于点 $M$.

(1)求证: $\triangle A D E \sim \triangle F M C$;
(2)求 $\angle A B F$ 的度数;
(3)若 $N$ 是 $A F$ 的中点, 如图 2, 求证: $N D=N O$.