单选题 (共 17 题 ),每题只有一个选项正确
$\frac{\log _8 9}{\log _2 3}$ 的值是
$\text{A.}$ $\frac{2}{3}$
$\text{B.}$ 1
$\text{C.}$ $\frac{3}{2}$
$\text{D.}$ 2
如果函数 $\mathrm{y}=\sin \left(\omega_{\mathrm{x}}\right) \cos \left(\omega_{\mathrm{x}}\right)$ 的最小正周期是 $4 \pi$, 那么常数 $\omega$ 为
$\text{A.}$ 4
$\text{B.}$ 2
$\text{C.}$ $\frac{1}{2}$
$\text{D.}$ $\frac{1}{4}$
极坐标方程分别是 $\rho=\cos \theta$ 和 $\rho=\sin \theta$ 的两个圆的圆心距是
$\text{A.}$ 2
$\text{B.}$ $\sqrt{2}$
$\text{C.}$ 1
$\text{D.}$ $\frac{\sqrt{2}}{2}$
方程 $\sin 4 x \cos 5 x=-\cos 4 x \sin 5 x$ 的一个解是
$\text{A.}$ $10^{\circ}$
$\text{B.}$ $20^{\circ}$
$\text{C.}$ $50^{\circ}$
$\text{D.}$ $70^{\circ}$
已知轴截面是正方形的圆柱的高与球的直径相等, 则圆柱的全面积与球的表面积的比是
$\text{A.}$ $6: 5$
$\text{B.}$ $5: 4$
$\text{C.}$ $4: 3$
$\text{D.}$ $3: 2$
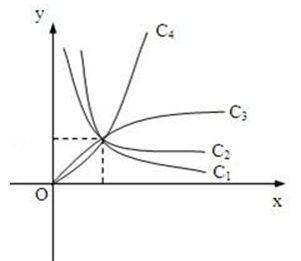
图中曲线是幂函数 ${y}=x^n$ 在第一象限的图象. 已知 $n$ 取 $\pm 2, \pm \frac{1}{2}$ 四个值, 则相应于曲线 ${c} 1 、 {c} 2 、 {c} 3 、 {c} 4$ 的 $n$ 依次为
$\text{A.}$ $-2,-\frac{1}{2},\frac{1}{2},2$
$\text{B.}$ $-2,2,\frac{1}{2},-\frac{1}{2}$
$\text{C.}$ $2,-2,-\frac{1}{2},\frac{1}{2}$
$\text{D.}$ $\frac{1}{2},-\frac{1}{2},2,-2$
若 $\log _{\mathrm{a}} 2 < \operatorname{logb} 2 < 0$, 则
$\text{A.}$ $0 < {a} < {b} < 1$
$\text{B.}$ $0 < {b} < {a} < 1$
$\text{C.}$ ${a}>{b}>1$
$\text{D.}$ $b>a>1$
直线 $\left\{\begin{array}{l}x=t \sin 20^{\circ}+3 \\ y=-t \sin 20^{\circ}\end{array}\right.$ ( $t$ 为参数) 的倾斜角是
$\text{A.}$ $20^{\circ}$
$\text{B.}$ $70^{\circ}$
$\text{C.}$ $45^{\circ}$
$\text{D.}$ $135^{\circ}$
在四棱锥的四个侧面中, 直角三角形最多可有
$\text{A.}$ 1 个
$\text{B.}$ 2 个
$\text{C.}$ 3 个
$\text{D.}$ 4 个
圆心在抛物线 ${y}^2=2 {x}$ 上, 且与 $x$ 轴和该抛物线的准线都相切的一个圆的方程是
$\text{A.}$ $ x^2+y^2-x-2 y-\frac{1}{4}=0$
$\text{B.}$ $x^2+y^2+x-2y+1=0$
$\text{C.}$ $x^2+y^2-x-2y+1=0$
$\text{D.}$ $ x^2+y^2-x-2 y+\frac{1}{4}=0$
在 $\left(x^2+3 x+2\right)^5$ 的展开式中 x 的系数为
$\text{A.}$ 160
$\text{B.}$ 240
$\text{C.}$ 360
$\text{D.}$ 800
已知直线 $l_1$ 和 $l_2$ 的夹角平分线为 $y=x$, 如果 $l_1$ 的方程是 $a x+b y+c=0$, 那么直线 $l_2$ 的方程为
$\text{A.}$ $b x+a y+c=0$
$\text{B.}$ $a x-b y+c=0$
$\text{C.}$ $b x+a y-c=0$
$\text{D.}$ $b x-a y+c=0$
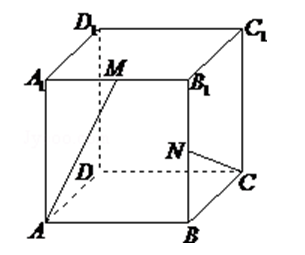
在棱长为 1 的正方体 $A B C D-A_1 B 1 C 1 D 1$ 中, $M$ 和 $N$ 分别为 $A 1 B 1$ 和 $B B 1$ 的中点,那么直线 AM 与 CN 所成角的余弦值是
$\text{A.}$ $\frac{\sqrt{3}}{2}$
$\text{B.}$ $\frac{\sqrt{10}}{10}$
$\text{C.}$ $\frac{3}{5}$
$\text{D.}$ $\frac{2}{5}$
已知复数 $z$ 的模为 2 , 则 $|z-i|$ 的最大值为
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ $\sqrt{5}$
$\text{D.}$ 3
函数 $\mathrm{y}=\frac{\mathrm{e}^{\mathrm{x}}+\mathrm{e}^{-\mathrm{x}}}{2}$ 的反函数
$\text{A.}$ 是奇函数,在 $(0,+\infty)$ 上是减函数
$\text{B.}$ 是偶函数,在 $(0,+\infty)$ 上是减函数
$\text{C.}$ 是奇函数,在 $(0,+\infty)$ 上是增函数
$\text{D.}$ 是偶函数,在 $(0,+\infty)$ 上是增函数
如果函数 ${f}({x})={x}^2+{bx}+{c}$ 对任意实数 t 都有 ${f}(2+{t})={f}(2-{t})$ ,那么
$\text{A.}$ ${f}(2) < {f}(1) < {f}(4)$
$\text{B.}$ ${f}(1) < {f}(2) < {f}(4)$
$\text{C.}$ ${f}(2) < {f}(4) < {f}(1)$
$\text{D.}$ ${f}(4) < {f}(2) < {f}(1)$
长方体的全面积为 11 , 十二条棱长度之和为 24 , 则这个长方体的一条对角线长为
$\text{A.}$ $2 \sqrt{3}$
$\text{B.}$ $\sqrt{14}$
$\text{C.}$ 5
$\text{D.}$ 6
填空题 (共 5 题 ),请把答案直接填写在答题纸上
方程 $\frac{1+3^{-x}}{1+3^x}=3$ 的解是
$\sin 15^{\circ} \sin 75^{\circ}$ 的值是
21. (3 分) 设含有 10 个元素的集合的全部子集数为 S , 其中由 3 个元素组成的子集数为 T ,则 $\frac{\mathrm{T}}{\mathrm{S}}$ 的值为
焦点为 $F_1(-2,0)$ 和 $F 2(6,0)$, 离心率为 2 的双曲线的方程是
已知等差数列 $\left\{a_n\right\}$ 的公差 $d \neq 0$, 且 a1, a3, a9 成等比数列, 则 $\frac{a_1+a_3+a_9}{a_2+a_4+a_{10}}$的值是
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知 $\mathrm{z} \in \mathrm{C}$, 解方程 ${z} \overline{{z}}-3 {i} \overline{{z}}=1+3 {i}$.
已知 $\frac{\pi}{2} < \beta < \alpha < \frac{3 \pi}{4}, \cos (\alpha-\beta)=\frac{12}{13}, \sin (\alpha+\beta)=-\frac{3}{5}$. 求 $\sin 2 a$ 的值.
已知: 两条异面直线 $a 、 b$ 所成的角为 $\theta$, 它们的公垂线段 $A A_1$ 的长度为 $d$. 在直线 $a 、 b$ 上分别取点 $E 、 F$, 设 $A 1 E=m, A F=n$. 求证: $E F=\sqrt{d^2+m^2+n^2 \pm 2 m n \cos \theta}$.
设等差数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 Sn . 已知 $\mathrm{a} 3=12, \mathrm{~S} 12>0, \mathrm{~S} 13 < 0$.
(1)求公差 d 的取值范围.
(2)指出 $\mathrm{S}_1, \mathrm{~S} 2, \cdots, \mathrm{S} 12$ 中哪一个值最大, 并说明理由.
已知椭圆 $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \quad(a>b>0), A 、 B$ 是椭圆上的两点, 线段 $A B$ 的垂直平分线与 x 轴相交于点 $\mathrm{P}(\mathrm{x} 0,0)$. 证明 $-\frac{a^2-b^2}{a} < x_0 < \frac{a^2-b^2}{a}$
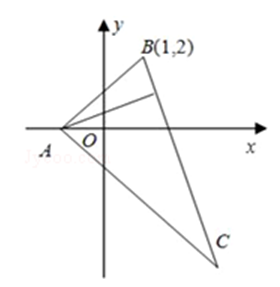
在 $\triangle \mathrm{ABC}$ 中, 已知 $B C$ 边上的高所在直线的方程为 $\mathrm{x}-2 \mathrm{y}+1=0, \angle \mathrm{A}$ 的平分线所在直线的方程为 $\mathrm{y}=0$. 若点 B 的坐标为 $(1,2)$, 求点 C 的坐标.