单选题 (共 10 题 ),每题只有一个选项正确
如果向东走 10 m 记作 +10 m , 那么向西走 8 m 记作
$\text{A.}$ $-10 m$
$\text{B.}$ $+10 m$
$\text{C.}$ $-8 m$
$\text{D.}$ $+8 m$
如图, 将 $\triangle A B C$ 沿 $B C$ 向右平移得到 $\triangle D E F$, 若 $B C=5, B E=2$, 则 $C F$ 的长是

$\text{A.}$ 2
$\text{B.}$ 2.5
$\text{C.}$ 3
$\text{D.}$ 5
某女鞋专卖占在一周内销售了某种女鞋 60 双, 对这批鞋子尺码及销量进行统计, 得到条形统计图 (如图). 根据图中信息, 建议下次进货量最多的女鞋尺码是

$\text{A.}$ 22 cm
$\text{B.}$ 22.5 cm
$\text{C.}$ 23 cm
$\text{D.}$ 23.5 cm
如图, 小兵同学从 $A$ 处出发向正东方向走 $x$ 米到达 $B$ 处, 再向正北方向走到 $C$ 处, 已知 $\angle B A C=\alpha$, 则 $A, C$ 两处相距

$\text{A.}$ $\frac{x}{\sin \alpha}$ 米
$\text{B.}$ $\frac{x}{\cos \alpha}$ 米
$\text{C.}$ $x \cdot \sin \alpha$ 米
$\text{D.}$ $x \cdot \cos \alpha$ 米
《孙子算经》记载: “今有木, 不知长短. 引绳度之, 余绳四尺五寸:屈绳量之, 不足一尺. 木长几何?”(尺、寸是长度单位, 1 尺=10 寸)。意思是, 现有一根长木, 不知道其长短. 用一根绳子去度量长木, 绳子还剩余 4.5 尺; 将绳子对折再度量长木, 长木还剩余 1 尺. 问长木长多少? 设长木长为 $x$ 尺, 则可列方程为
$\text{A.}$ $\frac{1}{2}(x+4.5)=x-1$
$\text{B.}$ $\frac{1}{2}(x+4.5)=x+1$
$\text{C.}$ $\frac{1}{2}(x-4.5)=x+1$
$\text{D.}$ $\frac{1}{2}(x-4.5)=x-1$
如图, 数学活动课上, 为测量学校旗杆高度, 小菲同学在脚下水平放置一平面镜, 然后向后退(保持脚、镜和旗杆底端在同一直线上), 直到她刚好在镜子中在到旗杆的顶端. 已知小菲的眼睛离地面高度为 1.6 m , 同时量得小菲与镜子的水平距离为 2 m , 镜子与旗杆的水平距离为 10 m , 则旗杆高度为

$\text{A.}$ 6.4 m
$\text{B.}$ 8m
$\text{C.}$ 9.6 m
$\text{D.}$ 12.5 m
若点 $P(m, n)$ 在抛物线 $y=a x^2(a \neq 0)$ 上, 则下列各点在抛物线 $y=a(x+1)^2$ 上的是
$\text{A.}$ $(m, n+1)$
$\text{B.}$ $(m+1, n)$
$\text{C.}$ $(m, n-1)$
$\text{D.}$ $(m-1, n)$
如图, 在 Rt $\triangle A B C$ 中, $\angle C=90^{\circ}, A C=6, A B=10$. 以点 $A$ 为圆心, 适当长为半径画弧, 分别交 $A C, A B$ 于点 $M, N$, 再分别以 $M, N$ 为圆心, 大于 $\frac{1}{2} M N$ 的长为半径两弧, 两弧在 $\angle C A B$的内部相交于点 $P$, 画射线 $A P$ 与 $B C$ 交于点 $D, D E \perp A B$, 垂足为 $E$. 则下列结论错误的是
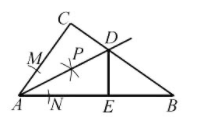
$\text{A.}$ $\angle C A D=\angle B A D$
$\text{B.}$ $C D=D E$
$\text{C.}$ $A D=5 \sqrt{3}$
$\text{D.}$ $C D: B D=3: 5$
关于 $x, y$ 的方程组 $\left\{\begin{array}{l}3 x+y=2 m-1, \\ x-y=n\end{array}\right.$ 的解满足 $x+y=1$, 则 $4^m \div 2^n$ 的值是
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 4
$\text{D.}$ 8
抛物线 $y=-x^2+k x+k-\frac{5}{4}$ 与 $x$ 轴的一个交点为 $A(m, 0)$, 若 $-2 \leqslant m \leqslant 1$, 则实数 $k$ 的取值范围是
$\text{A.}$ $-\frac{21}{4} \leqslant k \leqslant 1$
$\text{B.}$ $k \leqslant-\frac{21}{4}$ 或 $k \geqslant 1$
$\text{C.}$ $-5 \leqslant k \leqslant \frac{9}{8}$
$\text{D.}$ $k \leqslant-5$ 或 $k \geqslant \frac{9}{8}$
填空题 (共 6 题 ),请把答案直接填写在答题纸上
若 $\frac{x+1}{x-2}=0$, 则 $x$ 的值为
不透明袋中有红、白两种颜色的小球, 这些球除颜色外无其他差别. 从袋中随机取出一个球是红球的概率为 0.6 , 若袋中有 4 个白球, 则袋中红球有
如图, $A B$ 是 $\odot O$ 的直径, 点 $D, M$ 分别是弦 $A C$, 弧 $A C$ 的中点, $A C=12, B C=5$, 则 $M D$ 的长是

小伟用撬棍撬动一块大石头, 已知阻力和阻力臂分别为 1000 N 和 0.6 m , 当动力臂由 1.5 m 增加到 2 m 时, 携动这块石头可以节省 $\qquad$ N 的力.
(杠杆原理:阻力 $\times$ 阻力臂 $=$ 动力 $\times$ 动力臂)
如图, 直线 $y=k x-2 k+3$ ( $k$ 为常数, $k < 0$ ) 与 $x, y$ 轴分別交于点 $A, B$, 则 $\frac{2}{O A}+\frac{3}{O B}$ 的值是

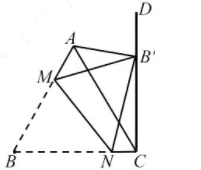
如图, 在等边 $\triangle A B C$ 中, 过点 $C$ 作射线 $C D \perp B C$, 点 $M, N$分别在边 $A B, B C$ 上, 将 $\triangle A B C$ 沿 $M N$ 折叠, 使点 $B$ 落在射线 $C D$ 上的点 $B^{\prime}$ 处, 连接 $A B^{\prime}$, 已知 $A B=2$. 给出下列四个结论: (1) $C N+N B^{\prime}$ 为定值; (2)当 $B N=2 N C$ 时, 四边形 $B M B^{\prime} N$为菱形:(3)当点 $N$ 与 $C$ 重合时, $\angle A B^{\prime} M=18^{\circ}$; (4)当 $A B^{\prime}$ 最短时, $M N=\frac{7 \sqrt{21}}{20}$. 其中正确的结论是 $\qquad$ . (填写序号)
解答题 (共 9 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
先化简, 再求值: $(a-2)(a+2)-(a+2)^2$, 其中 $a=-\frac{3}{2}$.
如图, 在 $\square A B C D$ 中, 点 $E, F$ 在对角线 $A C$ 上, $\angle C B E=\angle A D F$.
求证: (1) $A E=C F$. (2) $B E / / D F$.

为培养学生劳动习惯, 提升学生劳动技能, 某校在五月第二周开展了劳动教育实践周活动. 七 (1) 班提供了四类活动:A.物品整理,B.环境美化,C.植物栽培,D.工具制作. 要求每个学生选择其中一项活动参加, 该班数学科代表对全班学生参与四类活动情况进行了统计, 并绘制成统计图 (如图).
(1) 已知该班有 15 人参加 A 类活动, 则参加 C 类活动有多少人?
(2) 该班参加 D 类活动的学生中有2名女生和2名男生获得一等奖, 其中一名女生叫王朋, 若从获得一等奖的学生中随机抽取两人参加学校 “工具制作” 比赛, 求刚好抽中王丽和 1 名男生的概率.

已知关于 $x$ 的一元二次方程 $x^2-(2 m-1) x-3 m^2+m=0$.
(1)求证: 无论 $m$ 为何值, 方程总有实数根.
(2)若 $x_1, x_2$ 是方程的两个实数根, 且 $\frac{x_2}{x_1}+\frac{x_1}{x_2}=-\frac{5}{2}$, 求 $m$ 的值.
如图, 一次函数图象与反比例函数图象交于点 $A(-1,6)$, $B\left(\frac{3}{a}, a-3\right)$, 与 $x$ 轴交于点 $C$, 与 $y$ 轴交于点 $D$.
(1)求反比例函数与一次函数的解所式.
(2) 点 $M$ 在 $x$ 轴上, 若 $S_{\triangle O A M}=S_{\triangle O A B}$, 求点 $M$ 的坐标.

如图, $A B$ 与 $\odot O$ 相切于点 $A$, 半径 $O C / / A B, B C$ 与 $\odot O$ 相交于点 $D$, 连接 $A D$.
(1) 求证: $\angle O C A=\angle A D C$.
(2) 若 $A D=2, \tan B=\frac{1}{3}$, 求 $O C$ 的长.

某工厂计划从 $\mathrm{A}, \mathrm{B}$ 两种产品中选择一种生产并销售, 每日产销 $x$ 件. 已知 A 产品成本价 $m$ 元/件 ( $m$ 为常数, 且 $4 \leqslant m \leqslant 6$ ), 售价 8 元/件, 每日最多产销 500 件, 同时每日共支付专利费 30 元: B产品成本价 12 元/件, 售价 20 元/件, 每日最多产销 300 件, 同时每日支付专利费 $y$ 元, $y$ (元) 与每日产销 $x$ (件) 满足关系式 $y=80+0.01 x^2$.
(1) 若产销 $\mathrm{A}, \mathrm{B}$ 两种产品的日利润分别为 $w_1$ 元, $w_2$ 元, 请分别写出 $w_1, w_2$ 与 $x$ 的函数关系式, 并写出 $x$ 的取值范围.
(2) 分别求出产销 $\mathrm{A}, \mathrm{B}$ 两种产品的最大日利润. (A 产品的最大日利润用含 $m$ 的代数式表示)
(3) 为获得最大日利润, 该工厂应该选择产销哪种产品? 并说明理由.
【利润 $=$ (售价一成本 $) \times$ 产销数量一专利费】 ②
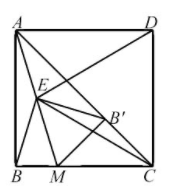
如图, 正方形 $A B C D$ 中, 点 $M$ 在边 $B C$ 上, 点 $E$ 是 $A M$ 的中点,连接 $E D, E C$.
(1) 求证: $E D=E C$.
(2) 将 $B E$ 绕点 $E$ 逆时针旋转, 使点 $B$ 的对应点 $B$ 落在 $A C$ 上,连接 $M B^{\prime}$. 当点 $M$ 在边 $B C$ 上运动时 (点 $M$ 不与 $B, C$ 重合),判断 $\triangle C M B^{\prime}$ 的形状, 并说明理由.
(3) 在 (2) 的条件下, 已知 $A B=1$, 当 $\angle D E B^{\prime}=45^{\circ}$ 时, 求 $B M$的长.
如图 1, 抛物线 $y=a x^2+b x+3(a \neq 0)$ 与 $x$ 轴交于 $A(-1,0), B(3,0)$ 两点, 与 $y$轴交于点 $C$.
(1) 求抛物线的解析式.
(2) 点 $P$ 在抛物线上, 点 $Q$ 在 $x$ 轴上, 以 $B, C, P, Q$ 为顶点的四边形为平行四边形,求点 $P$ 的坐标.
(3) 如图 2, 抛物线顶点为 $D$, 对称轴与 $x$ 轴交于点 $E$, 过点 $K(1,3$ ) 的直线(直线 $K D$ 除外) 与抛物线交于 $G, H$ 两点, 直线 $D G, D H$ 分别交 $x$ 轴于点 $M, N$. 试探究 $E M \cdot E N$ 是否为定值, 若是, 求出该定值; 若不是, 说明理由.