单选题 (共 6 题 ),每题只有一个选项正确
$\left(1 \frac{1}{2}\right)^0-\left(1-0.5^{-2}\right) \div \sqrt[3]{\left(\frac{27}{8}\right)^2}$ 的值为
$\text{A.}$ $-\frac{1}{3}$
$\text{B.}$ $\frac{1}{3}$
$\text{C.}$ $\frac{4}{3}$
$\text{D.}$ $\frac{7}{3}$
如图是指数函数(1) $y=a^x$ ,(2) $y=b^x$ ,(3) $y=c^x ,$ (4) $y=d^x$ 的图像,则 $a , b , c , d$ 与 0 和1的大小关系是
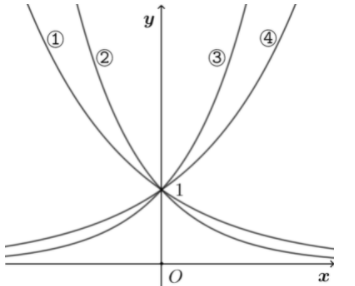
$\text{A.}$ $0 < a < b < 1 < c < d$
$\text{B.}$ $0 < b < a < 1 < d < c$
$\text{C.}$ $1 < a < b < c < d$
$\text{D.}$ $0 < a < b < 1 < d < c$
设 $a \log _3 4=2$ ,则 $4^{-a}=$
$\text{A.}$ $\frac{1}{16}$
$\text{B.}$ $\frac{1}{9}$
$\text{C.}$ $\frac{1}{8}$
$\text{D.}$ $\frac{1}{6}$
已知 $a=\log _5 2 , b=\log _{0.5} 0.2 , c=0.5^{0.2}$ ,则 $a, b, c$ 的大小关系为
$\text{A.}$ $a < c < b$
$\text{B.}$ $a < b < c$
$\text{C.}$ $b < c < a$
$\text{D.}$ $c < a < b$
设 $2^a=5^b=m$ ,且 $\frac{1}{a}+\frac{1}{b}=1$ ,则 $m=$
$\text{A.}$ $\sqrt{10}$
$\text{B.}$ 10
$\text{C.}$ 20
$\text{D.}$ 100
已知函数 $f(x)=\left\{\begin{array}{l}\mathrm{e}^x, x \leq 0 , \\ \ln x, x>0 ,\end{array}, g(x)=f(x)+x+a\right.$. 若 $g(x)$ 存在 2 个零点,则 $a$ 的取值范围是
$\text{A.}$ $[-1,0)$
$\text{B.}$ $[0,+\infty)$
$\text{C.}$ $[-1,+\infty)$
$\text{D.}$ $[1,+\infty)$
填空题 (共 1 题 ),请把答案直接填写在答题纸上
已知函数 $f(x)=\left\{\begin{array}{l}x+1, x \leq 0, \\ \log _2 x, x>0\end{array}\right.$ 则函数 $y=f[f(x)]$ 的所有零点之和为
解答题 (共 4 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知定义在 $(-1,1)$ 上的奇函数 $f(x)$. 在 $x \in(-1,0)$ 时, $f(x)=2^x+2^{-x}$.
(1)试求 $f(x)$ 的表达式;
(2) 若对于 $x \in(0,1)$ 上的每一个值,不等式 $t \cdot 2^x \cdot f(x) < 4^x-1$ 恒成立,求实数 $t$ 的取值范围.
已知函数 $f(x)=\lg (x+2)-\lg (2-x)$.
(1)求 $f(x)$ 的定义域;
(2)判断 $f(x)$ 的奇偶性并予以证明;
(3)求不等式 $f(x)>1$ 的解集.
已知函数 $y=f(x)(x \in R)$ 是偶函数. 当 $x \geq 0$ 时, $f(x)=x^2-4 x$.
(1) 求函数 $f(x)$ 在 $x \in R$ 上的解析式;
(2) 若函数 $f(x)$ 在区间 $[a, a+3]$ 上单调,求实数 $a$ 的取值范围;
(3)已知 $h(x)=|f(x)|-m$ ,试讨论 $h(x)$ 的零点个数,并求对应的 $m$ 的取值范围.
设函数 $y=f(x)$ 的定义域 $D \subseteq \mathrm{R}$, 若对任意 $x \in D$ ,均有 $f(-x) \neq-f(x)$ 成立,则称 $y=f(x)$ 为“无奇”函数.
(1)判断函数 ① $f(x)=x^2$ 和 ② $g(x)=\lg \frac{2-x}{1+x}$ 是否为“无奇”函数,说明理由;
(2) 若函数 $h(x)=3 x^3-2 x^2+x+a$ 是定义在 $[-1,2]$ 上的 “无奇”函数,求实数 $a$ 的取值范围;
(3) 若函数 $r(x)=\frac{1}{2^{x+1}+1}+m$ 是 “无奇”函数,求实数 $m$ 的取值范围.