解答题 (共 4 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设 $X_1, X_2, \cdots, X_n$ 为总体的一个样本, $x_1, x_2, \cdots, x_n$ 为一相应的样本值.求下列各总体的概率密度或分布律中的未知参数的矩估计量和矩估计值.
(1) $f(x)= \begin{cases}\theta c^\theta x^{-(\theta+1)}, & x>c \\ 0, & \text { 其他, }\end{cases}$其中 $c>0$ 为已知, $\theta>1, \theta$ 为末知参数.
(2) $f(x)= \begin{cases}\sqrt{\theta} x^{\sqrt{\theta}-1}, & 0 \leqslant x \leqslant 1 \\ 0, & \text { 其他, }\end{cases}$其中 $\theta>0, \theta$ 为未知参数.
(3) $P\{X=x\}=\left(\begin{array}{l}m \\ x\end{array}\right) p^x(1-p)^{m-x}, x=0,1,2, \cdots, m$,其中 $0 < p < 1, p$ 为未知参数.
设 $X_1, X_2, \cdots, X_n$ 为总体的一个样本, $x_1, x_2, \cdots, x_n$ 为一相应的样本值.求下列各参数的最大似然估计和估计量.
(1) $f(x)= \begin{cases}\theta c^\theta x^{-(\theta+1)}, & x>c \\ 0, & \text { 其他, }\end{cases}$其中 $c>0$ 为已知, $\theta>1, \theta$ 为末知参数.
(2) $f(x)= \begin{cases}\sqrt{\theta} x^{\sqrt{\theta}-1}, & 0 \leqslant x \leqslant 1 \\ 0, & \text { 其他, }\end{cases}$其中 $\theta>0, \theta$ 为未知参数.
(3) $P\{X=x\}=\left(\begin{array}{l}m \\ x\end{array}\right) p^x(1-p)^{m-x}, x=0,1,2, \cdots, m$,其中 $0 < p < 1, p$ 为未知参数.
(1)设总体X具有分布率
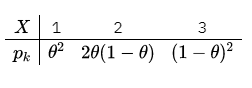
其中 $\theta(0 < \theta < 1)$ 为末知参数. 已知取得了样本值 $x_1=1, x_2=2, x_3=1$. 试求 $\theta$ 的矩估计值和最大似然估计值.
(2)设 $X_1, X_2, \cdots, X_n$ 是来自参数为 $\lambda$ 的泊松分布总体的一个样本, 试求 $\lambda$的最大似然估计量及矩估计量.
(3)设随机变量 $X$ 服从以 $r, p$ 为参数的负二项分布,其分布律为
$$
P\left\{X=x_k\right\}=\left(\begin{array}{c}
x_k-1 \\
r-1
\end{array}\right) p^r(1-p)^{x_k-r}, \quad x_k=r, r+1, \cdots,
$$
其中 $r$ 已知, $p$ 未知. 设有样本值 $x_1, x_2, \cdots, x_n$, 试求 $p$ 的最大似然估计值.
设某种电子器件的寿命 (以 $\mathrm{h}$ 计) $T$ 服从双参数的指数分布, 其概率密度为
$$
f(t)= \begin{cases}\frac{1}{\theta} \mathrm{e}^{-(t-c) / \theta}, & t \geqslant c, \\ 0, & \text { 其他, }\end{cases}
$$
其中 $c, \theta(c, \theta>0)$ 为未知参数. 自一批这种器件中随机地取 $n$ 件进行寿命试验.设它们的失效时间依次为 $x_1 \leqslant x_2 \leqslant \cdots \leqslant x_n$.
(1) 求 $\theta$ 与 $c$ 的最大似然估计值.
(2) 求 $\theta$ 与 $c$ 的矩估计量.