单选题 (共 8 题 ),每题只有一个选项正确
若复数 $\frac{3+a \mathrm{i}}{2-\mathrm{i}}$ 的实部与虚部相等, 则实数 $a$ 的值为
$\text{A.}$ 1
$\text{B.}$ 3
$\text{C.}$ -1
$\text{D.}$ -3
已知集合 $A=\{1,2,3\}, B=\left\{x \mid a < x < a^2\right\}$, 若 $A \subseteq B$, 则实数 $a$ 的取值范围是
$\text{A.}$ $(-\infty,-\sqrt{3}]$
$\text{B.}$ $(-\infty,-\sqrt{3})$
$\text{C.}$ $(-\sqrt{3}, 1)$
$\text{D.}$ $(-\infty,-\sqrt{3}) \cup(\sqrt{3},+\infty)$
如图为 2021 2022 年中国十大行业人工智能应用渗透率, 则下列说法错误的是
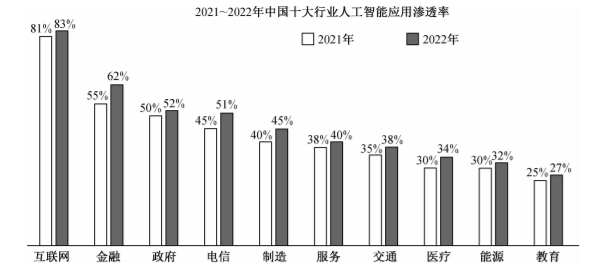
$\text{A.}$ 2021 年与 2022 年人工智能应用渗透率最低的行业都是教育
$\text{B.}$ 与 2021 年相比, 2022 年人工智能应用渗透率增长最快的是金融行业
$\text{C.}$ 2021 年十大行业人工智能应用渗透率的极差为 $56 \%$
$\text{D.}$ 2022 年十大行业人工智能应用渗透率的中位数是 $42.5 \%$
求值: $2 \sin 80^{\circ} \cos 20^{\circ}-\frac{\sin 20^{\circ}}{2 \sin 10^{\circ}}=$
$\text{A.}$ $\frac{\sqrt{3}}{3}$
$\text{B.}$ $\frac{\sqrt{2}}{2}$
$\text{C.}$ $1$
$\text{D.}$ $\frac{\sqrt{3}}{2}$
已知抛物线 $C_1: y^2=4 x$ 与抛物线 $C_2: x^2=4 y$, 则
$\text{A.}$ 过 $C_1$ 与 $C_2$ 焦点的直线方程为 $x+y=4$
$\text{B.}$ $C_1$ 与 $C_2$ 只有 1 个公共点
$\text{C.}$ 与 $x$ 轴平行的直线与 $C_1$ 及 $C_2$ 最多有 3 个交点
$\text{D.}$ 不存在直线与 $C_1$ 和 $C_2$ 都相切
若将 $\ln y=\ln x+\ln (y-x)$ 确定的两个变量 $y$ 与 $x$ 之间的关系看成 $y=f(x)$, 则函数 $y=$ $f(x)$ 的图象大致为
$\text{A.}$  $\text{B.}$
$\text{B.}$  $\text{C.}$
$\text{C.}$  $\text{D.}$
$\text{D.}$ 
中国古建筑的屋檐下常系挂风铃, 风吹铃动, 悦耳清脆, 亦称惊鸟铃. 若一个惊鸟铃由铜铸造而成, 且可近似看作由一个较大的圆椎挖去一个较小的圆椎, 两圆椎的轴在同一条直线上, 截面图如下, 其中 $O_1 O_3=20 \mathrm{~cm}, O_1 O_2=2 \mathrm{~cm}, A B=16 \mathrm{~cm}$, 若不考虑铃舌, 则下列数据比较接近该惊鸟铃质量的是 (参考数据: $\pi \approx 3$, 铜的密度为 $8.96 \mathrm{~g} / \mathrm{cm}^3$ )

$\text{A.}$ 1kg
$\text{B.}$ 2kg
$\text{C.}$ 3kg
$\text{D.}$ 0.5kg
若数列 $\left\{a_n\right\}$ 满足: 当 $\frac{k^2-k+2}{2} \leqslant n \leqslant \frac{k^2+k}{2}$ 时, $a_n=2^k\left(1+\frac{2}{k}\right)\left(k \in \mathbf{N}^*\right)$, 则数列 $\left\{a_n\right\}$ 的前 28 项和为
$\text{A.}$ 2048
$\text{B.}$ 2046
$\text{C.}$ 4608
$\text{D.}$ 4606
多选题 (共 3 题 ),每题有多个选项正确
已知椭圆 $C: \frac{x^2}{4}+y^2=1$ 的左、右焦点分别为 $F_1, F_2, P$ 是 $C$ 上一点, 则
$\text{A.}$ $\left|P F_1\right|+\left|P F_2\right|-\left|F_1 F_2\right|=4-\sqrt{3}$
$\text{B.}$ $\left|P F_1\right|\left|P F_2\right|$ 的最大值为 8
$\text{C.}$ $\left|\overrightarrow{P F_1}+\overrightarrow{P F_2}\right|$ 的取值范围是 $[2,4]$
$\text{D.}$ $\overrightarrow{P F_1} \cdot \overrightarrow{P F_2}$ 的取值范围是 $[-2,1]$
已知 $A, B$ 是随机事件, 若 $P(A+B)=1$ 且 $P(A \bar{B})=P(\bar{A} B)=\frac{1}{4}$, 则
$\text{A.}$ $P(A)=P(B)$
$\text{B.}$ $A, B$ 相互独立
$\text{C.}$ $P(A)=\frac{3}{4}$
$\text{D.}$ $P(B \mid A)=\frac{2}{3}$
已知点 $A\left(x_1, y_1\right), B\left(x_2, y_2\right)\left(x_1 \neq x_2\right)$ 是函数 $f(x)=a x+\sin 3 x(a \in \mathbf{R})$ 图象上两点, 则
$\text{A.}$ 对任意点 $A$, 存在无数个点 $B$, 使得曲线 $y=f(x)$ 在点 $A, B$ 处的切线倾斜角相等
$\text{B.}$ 若存在点 $A, B$, 使得曲线 $y=f(x)$ 在点 $A, B$ 处的切线垂直, 则 $-2 \sqrt{2} \leqslant a \leqslant 2 \sqrt{2}$
$\text{C.}$ 若对于任意点 $A, B$, 直线 $A B$ 的斜率恒小于 1 , 则 $a$ 的取值范围是 $(-\infty,-2)$
$\text{D.}$ 若 $x_1 x_2 \neq 0$ 且曲线 $y=f(x)$ 在点 $A, B$ 处的切线都过原点, 则 $\frac{\tan 3 x_1-\tan 3 x_2}{x_1-x_2}=3$
填空题 (共 3 题 ),请把答案直接填写在答题纸上
$\frac{(2 x-y)^6}{x^2 y^3}$ 的展开式中 $x$ 的系数为
已知函数 $f(x)=\sin \left(\omega x+\frac{\pi}{6}\right)(\omega>0)$, 对任意的 $x \in \mathbf{R}$, 都有 $f(x+\pi)=f(-x)$, 且 $f(x)$ 在区间 $\left(-\frac{\pi}{4}, \frac{\pi}{12}\right)$ 上单调, 则 $\omega$ 的值为
如图, 已知正方体 $A B C D-A_1 B_1 C_1 D_1$ 的棱长为 2 , 点 $E, F, G, H$ 分别为棱 $A A_1, A_1 D_1$, $A_1 B_1, B_1 C_1$ 的中点, 且点 $E, F, G, H$ 都在球 $O$ 的表面上, 点 $P$ 是球 $O$ 表面上的动点, 当点 $P$到平面 $A D D_1 A_1$ 的距离最大时, 异面直线 $P E$ 与 $G H$ 所成角的余弦值的平方为

解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
在 $\triangle A B C$ 中, 角 $A, B, C$ 的对边分别为 $a, b, c, \sin ^2 B+\sin ^2 C=\sin ^2 A+\sin B \sin C$.
(1) 若 $\triangle A B C$ 的面积 $S=2 \sqrt{3}, b+c=6$, 求 $a$ 的值;
(2) 若函数 $f(x)=3 x^2-4 x-\frac{\ln x}{\cos A}+1$ 在区间 $(0, t)$ 上有零点, 求 $t$ 的取值范围.
我国一科技公司生产的手机前几年的零部件严重依赖进口,2019 年某大国对其实施限制性策略, 该公司启动零部件国产替代计划, 与国内产业链上下游企业开展深度合作, 共同推动产业发展. 2023 年 9 月该公司最新发布的智能手机零部件本土制造比例达到了 $90 \%$, 该公司与一零部件制造公司合作生产某手机零部件, 为提高零部件质量, 该公司通过资金扶持与技术扶持, 帮助制造公司提高产品质量和竞争力, 同时派本公司技术人员进厂指导, 并每天随机从生产线上抽取一批零件进行质量检测. 下面是某天从生产线上抽取的 10 个零部件的质量分数(总分 1000 分, 分数越高质量越好): 928、933、945、950、959、967、967、975、982、 994. 假设该生产线生产的零部件的质量分数 $X$ 近似服从正态分布 $N\left(\mu, 20^2\right)$, 并把这 10 个样本质量分数的平均数 $\bar{x}$ 作为 $\mu$ 的值.
参考数据: 若 $X \sim N\left(\mu, \sigma^2\right)$, 则 $P(\mu-\sigma \leqslant X \leqslant \mu+\sigma) \approx 0.68$.
(1)求 $\mu$ 的值;
(2)估计该生产线上生产的 1000 个零部件中, 有多少个零部件的质量分数低于 940?
(3) 若从该生产线上随机抽取 $n$ 个零件中恰有 $\xi$ 个零部件的质量分数在 $[940,980]$ 内, 则 $n$ 为何值时, $P(\xi=10)$ 的值最大?
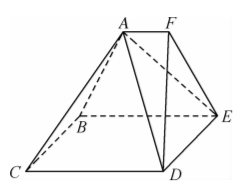
如图, 多面体 $A B C D E F$ 是由一个正四棱椎 $A-B C D E$ 与一个三棱椎 $F-A D E$ 拼接而成, 正四棱椎 $A-B C D E$ 的所有棱长均为 $3 \sqrt{2}, A F / / C D$.
(1) 在棱 $D E$ 上找一点 $G$, 使得平面 $A B C \perp$ 平面 $A F G$, 并证明你的结论;
(2) 若 $A F=\sqrt{2}$, 求直线 $D F$ 与平面 $A B C$ 所成角的正弦值.
已知双曲线 $C_1: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的一条渐近线与双曲线 $C_2: \frac{x^2}{4}-y^2=1$ 的一条渐近线垂直, 且 $C_1$ 的一个焦点到 $C_2$ 的一条渐近线的距离为 2 .
(1)求 $C_1$ 的方程;
(2) 若 $C_1$ 上任意一点 $A$ 关于直线 $y=x$ 的对称点为 $A^{\prime}$, 过 $A^{\prime}$ 分别作 $C_2$ 的两条渐近线的平行线,与 $C_2$ 分别交于 $P, Q$, 求证: $\left|A^{\prime} P\right| \cdot\left|A^{\prime} Q\right|$ 为定值.
同余定理是数论中的重要内容. 同余的定义为: 设 $a, b \in \mathbf{Z}, m \in \mathbf{N}^*$ 且 $m>1$.若 $m \mid a-b$ 则称 $a$ 与 $b$ 关于模 $m$ 同余, 记作 $a \equiv b(\bmod m)$ (“|”为整除符号).
(1) 解同余方程 $x^2-x \equiv 0(\bmod 3)$;
(2) 设 (1) 中方程的所有正根构成数列 $\left\{a_n\right\}$, 其中 $a_1 < a_2 < a_3 < \cdots < a_n$.
(1)若 $b_n=a_{n+1}-a_n\left(n \in \mathbf{N}^*\right)$, 数列 $\left\{b_n\right\}$ 的前 $n$ 项和为 $S_n$, 求 $S_{2024}$;
(2) 若 $c_n=\tan a_{2 n+1} \cdot \tan a_{2 n-1}\left(n \in \mathbf{N}^*\right)$, 求数列 $\left\{c_n\right\}$ 的前 $n$ 项和 $T_n$.