单选题 (共 8 题 ),每题只有一个选项正确
已知集合 $A=\{x \mid-1 < x < 3\}, B=\left\{x \in \boldsymbol{Z} \mid x^2-4 x < 0\right\}$, 则 $A \cap B=$
$\text{A.}$ $\{x \mid 0 < x < 3\}$
$\text{B.}$ $\{x \mid-1 < x < 3\}$
$\text{C.}$ $\{1,2\}$
$\text{D.}$ $\{0,1,2\}$
若 $\mathrm{i}$ 为虚数单位,复数 $z=\frac{1-\mathrm{i}}{\mathrm{i}}$, 则 $\bar{z}$ 等于
$\text{A.}$ $-1+\mathrm{i}$
$\text{B.}$ $-1-\mathrm{i}$
$\text{C.}$ $1+\mathrm{i}$
$\text{D.}$ $1-\mathrm{i}$
已知 $\boldsymbol{a}=(1,0),|\boldsymbol{b}|=1,|\boldsymbol{a}-\boldsymbol{b}|=1$, 则 $\boldsymbol{a}$ 与 $\boldsymbol{b}$ 的夹角为
$\text{A.}$ $\frac{\pi}{2}$
$\text{B.}$ $\frac{\pi}{4}$
$\text{C.}$ $\frac{\pi}{3}$
$\text{D.}$ $\frac{\pi}{6}$
将半径为 3 , 圆心角为 $\frac{2}{3} \pi$ 的扇形卷成一个圆锥的侧面, 则圆锥的体积为
$\text{A.}$ $\sqrt{2} \pi$
$\text{B.}$ $\frac{2 \sqrt{2}}{3} \pi$
$\text{C.}$ $\pi$
$\text{D.}$ $\frac{\pi}{3}$
设函数 $f(x)=a^{x^2-a x+1}(a>0$ 且 $a \neq 1)$ 在区间 $(0,1)$ 单调递减,则 $a$ 的取值范围是
$\text{A.}$ $(0,1)$
$\text{B.}$ $[2,+\infty)$
$\text{C.}$ $(0,1) \cup[2,+\infty)$
$\text{D.}$ $\left(0, \frac{1}{2}\right) \cup[2,+\infty)$
设函数 $f(x)=\cos \left(\omega x+\frac{\pi}{6}\right)-2(\omega>0)$ 的导函数 $f^{\prime}(x)$ 的最大值为 2 , 则 $f(x)$ 在 $\left[-\frac{\pi}{6}, \frac{\pi}{2}\right]$ 上的最小值为
$\text{A.}$ $\frac{\sqrt{3}}{2}-2$
$\text{B.}$ $-\frac{5}{2}$
$\text{C.}$ $-\frac{\sqrt{3}}{2}-2$
$\text{D.}$ $-3$
记非常数数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$, 设甲: $\left\{a_n\right\}$ 是等比数列; 乙: $S_n=B a_n+C(B \neq 0,1$,且 $C \neq 0$ ), 则
$\text{A.}$ 甲是乙的充要条件
$\text{B.}$ 甲是乙的充分不必要条件
$\text{C.}$ 甲是乙的必要不充分条件
$\text{D.}$ 甲是乙的既不充分也不必要条件
已知 $\alpha, \beta \in\left(0, \frac{\pi}{4}\right), \sin \alpha \cos \left(\frac{3 \pi}{2}+\alpha\right)-\sin \left(\frac{\pi}{2}+\alpha\right) \cos \alpha=-\frac{3}{5}$, 且 $3 \sin \beta=\sin (2 \alpha+\beta)$,则 $\alpha+\beta$ 的值为
$\text{A.}$ $\frac{\pi}{12}$
$\text{B.}$ $\frac{\pi}{6}$
$\text{C.}$ $\frac{\pi}{4}$
$\text{D.}$ $\frac{\pi}{3}$
多选题 (共 4 题 ),每题有多个选项正确
已知一组数据 $x_1, x_2, \cdots, x_{2023}$ 是公差不为 0 的等差数列, 若去掉数据 $x_{1012}$, 则所剩下的数据的
$\text{A.}$ 平均数不变
$\text{B.}$ 中位数不变
$\text{C.}$ 标准差不变
$\text{D.}$ 极差不变
根据《中华人民共和国噪声污染防治法》, 城市噪音分为工业生产噪音、建筑施工噪音、交通运输噪音和生活环境噪音等四大类。根据不同类型的噪音, 又进一步细化了限制标准。通常我们以分贝 (dB) 为单位来表示声音大小的等级, $30 \sim 40$ 分贝为安静环境,超过 50 分贝将对人体有影响, 90 分贝以上的环境会严重影响听力且会引起神经衰弱等疾病. 如果强度为 $v$ 的声音对应的分贝数为 $f(v)(\mathrm{dB})$, 那么满足: $f(v)=10 \times$ $\lg \frac{v}{1 \times 10^{-12}}$. 对几项生活环境的分贝数要求如下, 城市道路交通主干道: $60 \sim 70 \mathrm{~dB}$, 商业、工业混合区: $50 \sim 60 \mathrm{~dB}$, 安静住宅区、疗养院: $30 \sim 40 \mathrm{~dB}$. 已知在某城市道路交通主干道、工商业混合区、安静住宅区测得声音的实际强度分别为 $v_1, v_2, v_3$, 则
$\text{A.}$ $v_1 \geqslant v_2$
$\text{B.}$ $v_2>100 v_3$
$\text{C.}$ 若声音强度由 $v_1$ 降到 $v_3$, 需降为原来的 $\frac{1}{10}$
$\text{D.}$ 若要使分贝数由 40 提高到 60 , 则声音强度需变为原来的 100 倍
已知 $f(x)$ 是定义在 $\mathbf{R}$ 上的不恒为零的函数, 对于任意 $x, y \in \mathbf{R}$ 都满足 $f(x)-2=f(x+y)-f(y)$, 且 $f(x+1)$ 为偶函数, 则下列说法正确的是
$\text{A.}$ $f(0)=2$
$\text{B.}$ $f(x)$ 为奇函数
$\text{C.}$ $f(x)$ 关于点 $(0,2)$ 对称
$\text{D.}$ $\sum_{n=1}^{23} f(n)=46$
已知正四棱锥的侧棱长是 $x$, 正四棱雉的各个顶点均在同一球面上, 若该球的体积为 $\frac{4}{3} \pi$, 当 $x \in\left[\frac{\sqrt{2}}{2}, \sqrt{3}\right]$ 时,正四棱椎的体积可以是
$\text{A.}$ $\frac{1}{16}$
$\text{B.}$ $\frac{3}{4}$
$\text{C.}$ $\frac{4}{5}$
$\text{D.}$ $\frac{2}{3}$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
2024 年第 6 届 U23 亚洲杯将在卡塔尔举行. 现将甲、乙、丙、丁四名志愿者分配到 6 个项目中参加志愿活动, 且每名志愿者只能参加 1 个项目的志愿活动, 则有且只有 3 人分到同一项目中的情况有多少种. (用数字作答)
若将上底面半径为 2 , 下底面半径为 4 ,腰长为6的圆台型木块, 削成体积最大的球, 则该球的表面积为
设函数 $f(x)=2 \sin \left(\omega x+\frac{\pi}{3}\right)+1(\omega>0)$ 在区间 $(0, \pi)$ 内恰有两个零点, 则 $\omega$ 的取值范围是
函数 $f(x)=\sin \pi x+\ln |2 x-5|$ 的所有零点之和为
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
在 $\triangle A B C$ 中, 内角 $A, B, C$ 的对边分别是 $a, b, c$, 已知 $a \cos B+b \cos A-2 c \cos B=0$.
(1) 求内角 $B$ 的大小;
(2)若 $\triangle A B C$ 的面积为 $\frac{\sqrt{3}}{2}, a=2 c, \overrightarrow{A M}=\frac{1}{3} \overrightarrow{A C}$, 求线段 $B M$ 的长.
某班级为了提高学习数学、物理的兴趣, 组织了一次答题比赛活动, 规定每位学生共需回答 3 道题目. 现有两种方案供学生任意选择, 甲方案: 只选数学问题; 乙方案: 第一次选数学问题, 以后按如下规则选题, 若本次回答正确, 则下一次选数学问题,若回答错误, 则下一次选物理问题. 数学问题中的每个问题回答正确得 50 分, 否则得 0 分;物理问题中的每个问题回答正确得 30 分,否则得 0 分.
已知 $A$ 同学能正确回答数学问题的概率为 $\frac{1}{3}$, 能正确回答物理问题的概率为 $\frac{2}{3}$, 且能正确回答问题的概率与回答顺序无关.
(1)求 $A$ 同学采用甲方案答题, 得分不低于 100 分的概率;
(2) $A$ 同学选择哪种方案参加比赛更加合理,并说明理由.
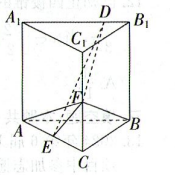
已知直三棱柱 $A B C-A_1 B_1 C_1$ 中, 侧面 $A A_1 B_1 B$ 为正方形, $A B=B C=2, E, F$ 分别为 $A C$ 和 $C C_1$ 的中点, $D$ 为棱 $A_1 B_1$ 上的点, 设 $B_1 D=m, B F \perp A_1 B_1$.
(1) 证明: $B F \perp D E$;
(2) 当 $m$ 为何值时, 平面 $B B_1 C_1 C$ 与平面 $D E F$ 的夹角的余弦值最大.
已知正项数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n, 2 \sqrt{S_n}=a_n+1$; 数列 $\left\{b_n\right\}$ 是递增的等比数列, 公比为 $q$, 且 $b_2, b_4$ 的等差中项为 $10, b_1, b_5$ 的等比中项为 8 .
(1) 求 $\left\{a_n\right\},\left\{b_n\right\}$ 的通项公式;
(2) 设 $c_n=\left\{\begin{array}{l}-a_n, n \text { 为奇数, } \\ \frac{3}{b_n}, n \text { 为偶数, }\end{array} T_n\right.$ 为 $\left\{c_n\right\}$ 的前 $n$ 项和, 若 $T_{2 n}+2 n^2-n+3 \geqslant \lambda b_n$ 能成立, 求实数 $\lambda$ 的最大值.
某学校新校区在校园里边种植了一种漂亮的植物, 会开出粉红色或黄色的花.这种植物第 1 代开粉红色花和黄色花的概率都是 $\frac{1}{2}$, 从第 2 代开始, 若上一代开粉红色的花, 则这一代开粉红色的花的概率是 $\frac{3}{5}$, 开黄色花的概率是 $\frac{2}{5}$; 若上一代开黄色的 - 花, 则这一代开粉红色的花的概率为 $\frac{1}{5}$, 开黄色花的概率为 $\frac{4}{5}$. 设第 $n$ 代开粉红色花的概率为 $P_n$.
(1)求第 2 代开黄色花的概率;
(2)证明: $\sum_{i=1}^n \frac{1-3 P_i}{5 P_i P_{i+1}} < 2$.
设 $f(x)=a x-(a+1) \ln x-\frac{1}{x}$ (其中 $a>0$ ).
(1) 讨论 $f(x)$ 的单调性;
(2) 设 $g(x)=x^2 \mathrm{e}^{2 x}-f(x)$, 若关于 $x$ 的不等式 $g(x) \geqslant a x+(a+3) \ln x+\frac{1}{x}+1$ 恒成立,求实数 $a$ 的取值范围.