单选题 (共 8 题 ),每题只有一个选项正确
复数 $\frac{5}{\mathrm{i}-2}$ 的共轭复数为
$\text{A.}$ $i+2$
$\text{B.}$ $i-2$
$\text{C.}$ $-2-\mathrm{i}$
$\text{D.}$ $2-\mathrm{i}$
已知集合 $A=\{x \mid 0 < x < 2\}, B=\left\{x \mid 4 x^2-4 x-15 < 0\right\}$, 则
$\text{A.}$ $\exists x \in A, x \notin B$
$\text{B.}$ $\forall x \in B, x \in A$
$\text{C.}$ $\exists x \in B, x \in A$
$\text{D.}$ $\forall x \in A, x \notin B$
指数函数 $y=a^x$ 的图象如图所示, 则 $y=a x^2+x$ 图象顶点横坐标的取值范围是
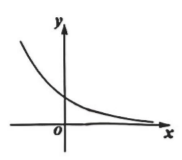
$\text{A.}$ $\left(-\infty,-\frac{1}{2}\right)$
$\text{B.}$ $\left(-\frac{1}{2}, 0\right)$
$\text{C.}$ $\left(0, \frac{1}{2}\right)$
$\text{D.}$ $\left(-\frac{1}{2},+\infty\right)$
在党中央的正确领导下, 我国坚定不移贯彻新发展理念, 着力推进高质量发展, 推动构建新发展格局, 实施供给侧结构性改革, 制定一系列具有全局性意义的区域重大战略, 经济实力实现历史性跃升. 国内生产总值 (GDP) 从五十四万亿元增长到一百一十四万亿元, 稳居世界第二位.下表是 2022 年我国大陆 31 省市区 GDP 数据.
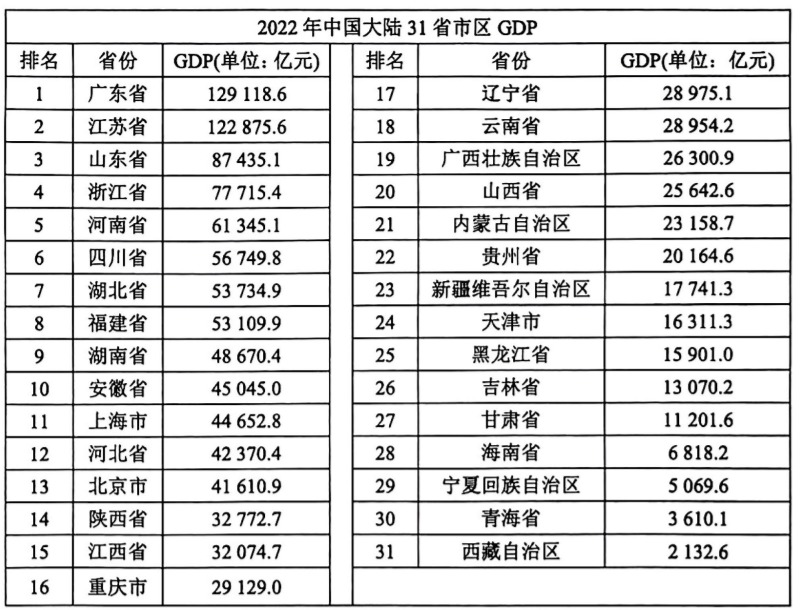
则由各省市区 GDP 组成的这组数据的第 75 百分位数为 (单位: 亿元)
$\text{A.}$ 16311.3
$\text{B.}$ 17741.3
$\text{C.}$ 48670.4
$\text{D.}$ 53109.9
已知 $\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c}$ 是同一平面内两两不共线的单位向量, 下列结论可能成立的是
$\text{A.}$ $b \cdot(a+c)=2$
$\text{B.}$ $(a+b) / /(a-b)$
$\text{C.}$ 存在不全为 0 的实数 $\lambda, \mu$, 使 $\lambda a+\mu b=0$
$\text{D.}$ 若 $a+b+c=0$, 则 $|a-b|=\sqrt{3}$
某地区有 20000 名考生参加了高三第二次调研考试. 经过数据分析, 数学成绩 $X$ 近似服从正态分布 $N\left(72,8^2\right)$, 则数学成绩位于 $[80,88]$ 的人数约为
参考数据: $P(\mu-\sigma \leqslant X \leqslant \mu+\sigma) \approx 0.6827, P(\mu-2 \sigma \leqslant X \leqslant \mu+2 \sigma) \approx 0.9545$, $P(\mu-3 \sigma \leqslant X \leqslant \mu+3 \sigma) \approx 0.9973$.
$\text{A.}$ 455
$\text{B.}$ 2718
$\text{C.}$ 6346
$\text{D.}$ 9545
如图,在棱长为1的正方体$ABCD-A_1B_1C_1D_1$中,$M$是$A_1B_1$的中点,点$P$是侧面$CDD_1C_1$上的动点,且$MP//AB_1C$, 则线段$MP$长度的取值范围为

$\text{A.}$ $\left[\frac{\sqrt{6}}{2}, \sqrt{2}\right]$
$\text{B.}$ $\left[1, \frac{\sqrt{6}}{2}\right]$
$\text{C.}$ $\left[\frac{\sqrt{6}}{2}, \frac{3}{2}\right]$
$\text{D.}$ $\left[\sqrt{2}, \frac{3}{2}\right]$
已知 $f(x)=\sqrt{\ln x+9 x-a}, a \in \mathbf{R}$, 曲线 $y=\cos x+2$ 上存在点 $\left(x_0, y_0\right)$, 使得 $f\left(f\left(y_0\right)\right)=y_0$, 则 $a$ 的范围是
$\text{A.}$ $(8,18+\ln 3)$
$\text{B.}$ $[8,18+\ln 3]$
$\text{C.}$ $(9,27+\ln 3)$
$\text{D.}$ $[9,27+\ln 3]$
多选题 (共 4 题 ),每题有多个选项正确
已知曲线 $C_1: 5 x^2+y^2=5, C_2: x^2-4 y^2=4$, 则
$\text{A.}$ $C_1$ 的长轴长为 $\sqrt{5}$
$\text{B.}$ $C_2$ 的渐近线方程为 $x \pm 2 y=0$
$\text{C.}$ $C_1$ 与 $C_2$ 的离心率互为倒数
$\text{D.}$ $C_1$ 与 $C_2$ 的焦点相同
已知 $\left\{a_n\right\}$ 为等差数列, 的 $n$ 项和为 $S_n, a_1=10$, 公差 $d=-2$, 则
$\text{A.}$ $S_4=S_7$
$\text{B.}$ 当 $n=5$ 或 6 时, $S_n$ 取得最小值为 30
$\text{C.}$ 数列 $\left\{\left|a_n\right|\right\}$ 的前 10 项和为 50
$\text{D.}$ 当 $n \leqslant 2023$ 时, $\left\{a_n\right\}$ 与数列 $\{3 m+10\}\left(m \in N^*\right)$ 共有 671 项互为相反数
已知函数 $f(x)=A \sin (\omega x+\varphi)\left(A>0, \omega>0,0 < \varphi < \frac{\pi}{2}\right)$ 的图象过点 $M\left(0, \frac{A}{2}\right)$和 $N(\pi, 0), f(x)$ 的最小正周期为 $T$, 则
$\text{A.}$ $T$ 可能取 $\frac{12 \pi}{7}$
$\text{B.}$ $f(x)$ 在 $(0,4 \pi)$ 上至少有 3 个零点
$\text{C.}$ 直线 $x=\frac{8 \pi}{11}$ 可能是曲线 $y=f(x)$ 的一个对称轴
$\text{D.}$ 若函数 $f(x)$ 的图象在 $[0,2 \pi]$ 上的最高点和最低点共有 4 个, 则 $\omega=\frac{11}{6}$
已知函数 $f(x)=(x-1)^3-a x-b+1$, 则下列结论正确的是
$\text{A.}$ 当 $a=3$ 时, 若 $f(x)$ 有三个零点, 则 $b$ 的取值范围为 $(-4,0)$
$\text{B.}$ 若 $f(x)$ 满足 $f(2-x)=3-f(x)$, 则 $a+b=-1$
$\text{C.}$ 若过点 $(2, m)$ 可作出曲线 $g(x)=f(x)-3 x+a x+b$ 的三条切线, 则 $-5 < m < -4$
$\text{D.}$ 若 $f(x)$ 存在极值点 $x_0$, 且 $f\left(x_0\right)=f\left(x_1\right)$, 其中 $x_0 \neq x_1$, 则 $x_1+2 x_0=3$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
满足圆 $x^2+(y-4)^2=25$ 与 $(x-a)^2+y^2=1$ 相交的一个 $a$ 值为
已知三棱雉 $P-A B C$ 的三条侧棱两两垂直, 且其外接球半径为 2 , 则 $S_{\triangle P A B}+S_{\triangle P A C}$ $+S_{\triangle P B C}$ 的最大值为
一个袋子中有 100 个大小相同的球, 其中有 40 个黄球, 60 个白球. 采取不放回摸球,从中随机摸出 22 个球作为样本, 用 $X$ 表示样本中黄球的个数. 当 $P(X=k)$ 最大时, $E(X)+k=$
已知点 $A(1,2)$ 在抛物线 $y^2=2 p x$ 上, 过点 $A$ 作圆 $(x-2)^2+y^2=2$ 的两条切线分别交抛物线于 $B, C$ 两点, 则直线 $B C$ 的方程为
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知 $\triangle A B C$ 的内角 $A, B, C$ 的对边分别为 $a, b, c$, 向量 $\boldsymbol{m}=(a, \sqrt{3} b)$, $\boldsymbol{n}=\left(\cos \left(\frac{\pi}{2}-B\right), \cos (\pi-A)\right)$, 且 $\boldsymbol{m} \perp \boldsymbol{n}$.
(1) 求 $A$;
(2) 若 $c=3, \triangle A B C$ 的面积为 $\frac{3 \sqrt{3}}{2}$, 求 $a$.
已知数列 $\left\{a_n\right\}$ 的首项 $a_1=3$, 且满足 $a_{n+1}+2 a_n=2^{n+2}$.
(1) 证明: $\left\{a_n-2^n\right\}$ 为等比数列;
(2)已知 $b_n=\left\{\begin{array}{ll}a_n, & n \text { 为奇数, } \\ \log _2 a_n, & n \text { 为偶数. }\end{array} T_n\right.$ 为 $\left\{b_n\right\}$ 的前 $n$ 项和, 求 $T_{10}$.
在四棱椎 $P-A B C D$ 中, 底面 $A B C D$ 是矩形, $P A \perp$ 平面 $A B C D, P A=A D=8 . M$为线段 $P D$ 上一点 ( $M$ 不与 $D$ 重合), 且 $A M \perp M C$.
(1) 证明: $M$ 为 $P D$ 的中点;
(2) 若平面 $B A M$ 与平面 $C A M$ 夹角的余弦值为 $\frac{\sqrt{3}}{3}$, 求 $A B$.

某市正在创建全国文明城市, 学校号召师生利用周末从事创城志愿活动. 高三 (1) 班一组有男生 4 人, 女生 2 人, 现随机选取 2 人作为志愿者参加活动, 志愿活动共有交通协管员、创建宜传员、文明监督员三项可供选择. 每名女生至多从中选择参加 2 项活动, 且选择参加 1 项或 2 项的可能性均为 $\frac{1}{2}$; 每名男生至少从中选择参加 2 项活动, 且选择参加 2 项或 3 项的可能性也均为 $\frac{1}{2}$. 每人每参加 1 项活动可获得综合评价 10 分, 选择参加几项活动彼此互不影响, 求
(1) 在有女生参加活动的条件下, 恰有一名女生的概率;
(2) 记随机选取的两人得分之和为 $X$, 求 $X$ 的期望.
已知双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的右焦点为 $F(2,0)$, 一条渐进线方程为
$$
y=\sqrt{3} x
$$
(1) 求 $C$ 的方程;
(2) 在 $x$ 轴上是否存在与 $F$ 不重合的点 $P$, 使得当过点 $F$ 的直线与 $C$ 的右支交于 $A$, $B$ 两点时, $\frac{|A F|}{|B F|}=\frac{|A P|}{|B P|}$ 总成立? 若存在, 求出点 $P$ 的坐标; 若不存在, 请说明理由.
已知函数 $f(x)=\mathrm{e}^x \sin x-x$.
(1) 当 $x \leqslant \frac{\pi}{2}$ 时, 求证: $f(x) \geqslant 0$;
(2) 当 $x>0$ 时, 函数 $f(x)$ 的零点从小到大依次排列, 记为 $\left\{x_n\right\}\left(n \in \mathbf{N}^*\right)$
证明: ① $\sin x_n>\sin x_{n+1}$; ② $x_{2 n-1}+\pi < 2 n \pi < x_{2 n}$.