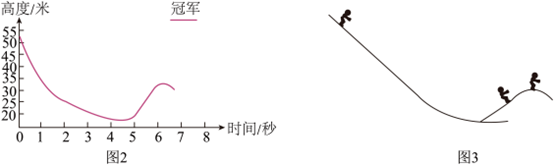
2022年北京冬奥会自由式滑雪女子大跳台比赛中,中国队运动员谷爱凌力压世界排名第一的选手,最后一跳以向左偏轴转体1620°的动作完美逆转(如图1),获得个人首金。大跳台比赛比赛场地分为助滑区、起跳台、着陆坡和终点区域四个部分。图2是某技术公司对谷爱凌夺冠一跳的“高度-时间”分析。已知谷爱凌及身上的装置总质量为m=65kg。根据这些信息回答下述问题
(1)不考虑运动员转体的动作,将运动员看做质点。
a、设助滑出发区距地面高度为h_1,运动员从静止出发,从起跳台起跳后能达到的最大高度距地面为h_2,不计人体能量的消耗、不计一切摩擦,求运动员在最高点的速度大小v(用字母表示);
b、请你根据图2中的信息,估算v大小;
c、运动员落到着陆坡时, 垂直坡面方向的速度在极短时间内减为 0 , 因此运动员要承受极 大的冲击力。设运动员在最高点速度约为 $v=20 \mathrm{~m} / \mathrm{s}$, 落到着陆坡时的速度方向与水平成 $\alpha=$ $45^{\circ}$. 着陆坡的倾角 $\theta=36^{\circ}$, 雪板与坡面经大约 $\Delta t=0.05 s$ 的撞击时间后继续滑行。请根据 以上条件估算运动员受到的冲击力。(保留 1 位有效数字) (可能会用到数据: $\sin 36^{\circ}=$ $\left.0.59, \cos 36^{\circ}=0.81, \sin 9^{\circ}=0.16, \sin 81^{\circ}=0.99\right)$ (提示, 先写表达式, 再代数)。
(2) 考虑运动员的转体动作。
$a$ 、若谷爱凌在空中腾空的时间约为 $3 \mathrm{~s}$, 在空中转动的角速度几乎不变, 求她在空中转动 的角速度大小;
$b$ 、物体转动动能可以理解为各部分绕轴转动的动能之和。已知物体转动的惯性用物理量 $I$ 来描述, 它的名称为 “转动惯量”, 物体转动的快慢用角速度 $\omega$ 描述。请类比质点动能表达 式 $E_k=\frac{1}{2} m v^2$, 写出物体转动动能表达式;
c、若将谷爱凌在空中转动, 理想化为一个半径约为 $0.20 \mathrm{~m}$ 的圆柱体的转动, 已知圆柱体的 转动惯量为 $I=\frac{1}{2} m R^2$ ( $m$ 为圆柱体质量, $R$ 为圆柱体半径), 并假设谷爱凌在冲出跳台的瞬 间 (约 $0.02 \mathrm{~s}$ ) 内获得足够的角速度, 请问她瞬间转体爆发的功率大约多大? (保留 1 位有 效数字)。