单选题 (共 8 题 ),每题只有一个选项正确
数列 $\left\{a_n\right\}$ 满足 $a_{n+1}=\frac{1}{1-a_n}, a_1=3$, 则 $a_{2021}=(\quad)$
$\text{A.}$ $-\frac{1}{2}$
$\text{B.}$ $\frac{2}{3}$
$\text{C.}$ $\frac{5}{2}$
$\text{D.}$ $3$
直线 $x \cos \alpha+\sqrt{3} y+2=0$ 的倾斜角的范围是
$\text{A.}$ $\left[0, \frac{\pi}{6}\right] \bigcup\left[\frac{5 \pi}{6}, \pi\right)$
$\text{B.}$ $\left[0, \frac{5 \pi}{6}\right]$
$\text{C.}$ $\left[\frac{\pi}{6}, \frac{\pi}{2}\right) \cup\left(\frac{\pi}{2}, \frac{5 \pi}{6}\right]$
$\text{D.}$ $\left[\frac{\pi}{6}, \frac{5 \pi}{6}\right]$
与双曲线 $y^2-\frac{x^2}{4}=1$ 有相同的焦点, 且短半轴长为 $2 \sqrt{5}$ 的椭圆方程是
$\text{A.}$ $\frac{y^2}{45}+\frac{x^2}{20}=1$
$\text{B.}$ $\frac{y^2}{85}+\frac{x^2}{80}=1$
$\text{C.}$ $\frac{x^2}{25}+\frac{y^2}{20}=1$
$\text{D.}$ $\frac{y^2}{25}+\frac{x^2}{20}=1$
等比数列 $\left\{a_n\right\}$ 的各项均为实数, 其前 $n$ 项和为 $S_n$, 已知 $S_3=14, S_6=\frac{63}{4}$, 则 $a_5=$
$\text{A.}$ $2$
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ $4$
$\text{D.}$ $\frac{1}{4}$
已知点 $F$ 为抛物线 $C: y^2=2 p x(p>0)$ 的焦点, 过点 $F$ 且倾斜角为 $60^{\circ}$ 的直线交抛物线 $C$ 于 $A, B$ 两点, 若 $|F A| \cdot|F B|=3$, 则 $p=$
$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ $1$
$\text{C.}$ $\frac{3}{2}$
$\text{D.}$ $2$
若 $M, N$ 为圆 $C:(x-2)^2+(y-2)^2=1$ 上任意两点, $P$ 为直线 $3 x+4 y-4=0$ 上一个动点, 则 $\angle M P N$ 的最大值是
$\text{A.}$ $45^{\circ}$
$\text{B.}$ $60^{\circ}$
$\text{C.}$ $90^{\circ}$
$\text{D.}$ $120^{\circ}$
在平面直角坐标系中, 定义 $|x|+|y|$ 称为点 $P(x, y)$ 的 “ $\delta$ 和”, 其中 $O$ 为坐标原点, 对
于下列结论: (1) “ $\delta$ 和” 为 1 的点 $P(x, y)$ 的轨迹围成的图形面积为 2 ; (2) 设 $P$ 是直
线 $2 x-y-4=0$ 上任意一点, 则点 $P(x, y)$ 的 “ $\delta$ 和” 的最小值为 2 ; (3)设 $P$ 是直线
$a x-y+b=0$ 上任意一点, 则使得 “ $\delta$ 和” 最小的点有无数个” 的充要条件是 $a=1$;
设 $P$ 是椭圆 $x^2+\frac{y^2}{2}=1$ 上任意一点, 则 “ $\delta$ 和”的最大值为 $\sqrt{3}$. 其中正确的结论序号为
$\text{A.}$ (1) (2) (3)
$\text{B.}$ (1) (2) (4)
$\text{C.}$ (1) (3) (4)
$\text{D.}$ (2) (3)(4)
若数列 $\left\{a_n\right\},\left\{b_n\right\}$ 的通项公式分别是 $a_n=(-1)^{n+2014} a, b_n=2+\frac{(-1)^{n+2015}}{n}$, 且 $a_n < b_n$ 对任 意 $n \in N^*$ 恒成立, 则实数 $a$ 的取值范围是
$\text{A.}$ $\left[-1, \frac{1}{2}\right)$
$\text{B.}$ $\left[-1, \frac{3}{2}\right)$
$\text{C.}$ $\left[-2, \frac{1}{2}\right)$
$\text{D.}$ $\left[-2, \frac{3}{2}\right)$
多选题 (共 4 题 ),每题有多个选项正确
分别抛郑两枚质地均匀的硬币, 设事件 $A=$ “第一枚正面朝上”, 事件 $B=$ “第二枚正面 朝上” , 则下列结论正确的是
$\text{A.}$ $P(A)=\frac{1}{2}$
$\text{B.}$ $P(A B)=\frac{1}{4}$
$\text{C.}$ 事件 $\mathrm{A}$ 与 $\mathrm{B}$ 互斥
$\text{D.}$ 事件 $\mathrm{A}$ 与 $B$ 相互独立
关于等差数列和等比数列, 下列四个选项中不正确的有
$\text{A.}$ 若数列 $\left\{a_n\right\}$ 的前 $n$ 项和 $S_n=a n^2+b n+c\left(a, b, c\right.$ 为常数) 则数列 $\left\{a_n\right\}$ 为等差数列
$\text{B.}$ 若数列 $\left\{a_n\right\}$ 的前 $n$ 项和 $S_n=2^{n+1}-2$, 则数列 $\left\{a_n\right\}$ 为等差数列
$\text{C.}$ 数列 $\left\{a_n\right\}$ 是等差数列, $S_n$ 为前 $n$ 项和, 则 $S_n, S_{2 n}-S_n, S_{3 n}-S_{2 n}, \cdots$ 仍为等差数列
$\text{D.}$ 数列 $\left\{a_n\right\}$ 是等比数列, $S_n$ 为前 $n$ 项和, 则 $S_n, S_{2 n}-S_n, S_{3 n}-S_{2 n}, \cdots$ 仍为等比数列;
已知正方体 $A B C D-A_1 B_1 C_1 D_1$ 的棱长为 $2, M$ 为 $D D_1$ 的中点, $N$ 为平面 $A B C D$ 内一动点,
则下列命题正确的有
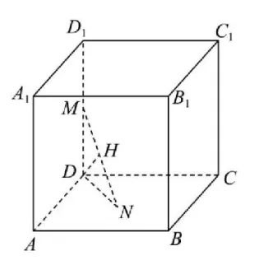
$\text{A.}$ 若 $M N=2$, 则 $M N$ 的中点的轨迹所围成图形的面积为 $\pi$
$\text{B.}$ 若 $M N$ 与平面 $A B C D$ 所成的角为 $\frac{\pi}{3}$, 则 $N$ 的轨迹为圆
$\text{C.}$ 若 $N$ 到直线 $B B_1$ 与直线 $D C$ 的距离相等, 则 $N$ 的轨迹为抛物线
$\text{D.}$ 若 $D_1 N$ 与 $A B$ 所成的角为 $\frac{\pi}{3}$, 则 $N$ 的轨迹为双曲线
已知椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的左, 右焦点分别是 $F_1, F_2$, 其中 $\left|F_1 F_2\right|=2 c$. 直线 1 过左焦点 $F_1$ 与椭圆交于 $A, B$ 两点,则下列说法中正确的有
$\text{A.}$ 若存在 $\triangle A B F_2$, 则 $\triangle A B F_2$ 的周长为 $4 a$
$\text{B.}$ 若 $A B$ 的中点为 $M$, 则 $k_{O M} \cdot k=\frac{b^2}{a^2}$
$\text{C.}$ 若 $\overrightarrow{A F_1} \cdot \overrightarrow{A F_2}=3 c^2$, 则椭圆的离心率的取值范围是 $\left[\frac{\sqrt{5}}{5}, \frac{1}{2} \mid\right.$
$\text{D.}$ 若 $|A B|$ 的最小值为 $3 c$, 则椭圆的离心率 $e=\frac{1}{3}$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
设点 $M$ 在直线 $x+y-1=0$ 上, $\odot M$ 与 $y$ 轴相切, 且经过点 $(-2,2)$, 则 $\odot M$ 的半径为
如果一个数列从第 2 项起, 每一项与它前一项的和除以与它前一项的差等于同一个常数, 那么这个数列就叫做 “和差等比数列” . 已知 $\left\{a_n\right\}$ 是 “和差等比数列” , $a_1=2, a_2=3$, 则使得不等式 $a_n>10$ 的 $n$ 的最小值是
已知圆 $(x-2)^2+y^2=9$ 与 $x$ 轴的交点分别为双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的顶点和 焦点, 设 $F_1, F_2$ 分别为双曲线 $C$ 的左、右焦点, $P$ 为 $C$ 右支上任意一点, 则 $\frac{\left|P F_1\right|^2}{\left|P F_2\right|^2+4}$ 的 取值范围为
在棱长为 1 的正方体 $A B C D-A_1 B_1 C_1 D_1$ 中, $P$ 是线段 $B C_1$ 上的点, 过 $A_1$ 的平面 $a$ 与直线 $P D$ 垂 直, 当 $P$ 在线段 $B C_1$ 上运动时, 平面 $a$ 截正方体 $A B C D-A_1 B_1 C_1 D_1$ 所得截面面积的最小值是
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知线段 $A B$ 的端点 $B(4,3)$, 端点 $\mathrm{A}$ 在圆 $C:(x+1)^2+y^2=4$ 上运动.
(1) 点 $M$ 在线段 $A B$ 上, 且 $\overrightarrow{A M}=\frac{1}{3} \overrightarrow{A B}$, 求点 $M$ 的轨迹方程;
(2) 若直线 $y=k(x-2)$ 与点 $M$ 的轨迹相交, 求实数 $k$ 的取值范围.
甲、乙两人加工一批标准直径为 $50 \mathrm{~mm}$ 的钢球共 1500 个, 其中甲加工了 600 个, 乙加工 了 900 个. 现分别从甲、乙两人加工的钢球中各抽取 50 个进行误差检测, 其结果如下:

(1) 估计这批钢球中直径误差不超过 $\pm 0.1 \mathrm{~mm}$ 的钢球的个数;
(2) 以甲、乙各自加工的钢球的总数为依据按分层抽样的方法从直径误差为 $-0.2 \mathrm{~mm}$ 的钢球中抽取 5 个, 再从这 5 个钢球中随机抽取 2 个, 求这 2 个钢球都是乙加工的概率;
(3) 你认为甲、乙两人谁加工的钢球更符合标准? 并说明理由.
已知双曲线 $\mathrm{C}$ 的焦点 $\mathrm{F}(2,0)$ 和离心率 $\mathrm{e}=\frac{2 \sqrt{3}}{3}$.
(1) 求双曲线 C 的方程;
(2) 若直线 $1: \mathrm{y}=\mathrm{kx}+\sqrt{2}$ 与曲线 $\mathrm{C}$ 恒有两个不同的交点 $\mathrm{A}$ 和 $\mathrm{B}$, 且 $\overrightarrow{O A} \overrightarrow{O B}>2$, 求 $\mathrm{k}$ 的取值范围.
已知正项数列 $\left\{a_n\right\}$ 的前 $n$ 项和 $S_n$, 满足 $S_n=2 a_n-2\left(n \in \mathrm{N}^*\right)$, 数列 $\left\{b_n\right\}$ 的前 $n$ 项积为 $n !$.
$$
(n !=1 \times 2 \times 3 \times \cdots \times n)
$$
(1) 求数列 $\left\{a_n\right\}$ 的通项公式;
(2) 令 $c_n=a_n b_n$, 求数列 $\left\{\frac{c_{n+2}}{c_n c_{n+1}}\right\}$ 的前 $n$ 项和.
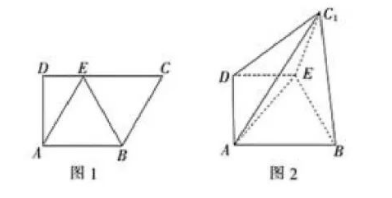
图 1 是直角梯形 $A B C D, A B / / C D, \angle D=90^{\circ}$, 四边形 $A B C E$ 是边长为 2 的菱形, 并且 $\angle$ $B C E=60^{\circ}$, 以 $B E$ 为折痕将 $\triangle B C E$ 折起, 使点$C$ 到达 $C_1$ 的位置, 且 $A C_1=\sqrt{6}$.
(1) 求证: 平面 $B C_1 E \perp$ 平面 $A B E D$.
(2) 在棱 $D C_1$ 上是否存在点 $P$, 使得点 $P$ 到平面
$A B C_1$ 的距离为 $\frac{\sqrt{15}}{5}$ ? 若存在, 求出直线 $E P$ 与平面 $A B C_1$ 所成角的正弦值; 若不存在, 请说
明理由.
已知椭圆 $C_1: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的离心率为 $\frac{1}{2}, P\left(1, \frac{3}{2}\right)$ 为椭圆上一点, $A, B$ 为椭 圆上不同两点, $O$ 为坐标原点,
(1) 求椭圆 $C$ 的方程;
(2) 线段 $A B$ 的中点为 $M$, 当 $\triangle A O B$ 面积取最大值时, 是否存在两定点 $G, H$, 使 $|G M|+|H M|$ 为定值? 若存在, 求出这个定值; 若不存在, 请说明理由.