单选题 (共 3 题 ),每题只有一个选项正确
甲袋中有 4 只红球, 有 6 只白球, 乙袋中有 6 只红球, 10 只白球, 现从两袋中各任取 1 球, 则 2 个球颜色相同的概率是
$\text{A.}$ $\frac{6}{40}$
$\text{B.}$ $\frac{15}{40}$
$\text{C.}$ $\frac{21}{40}$
$\text{D.}$ $\frac{19}{40}$
设随机变量 $X$ 服从 $N\left(27,0.2^2\right)$ 分布, 则其浙近线在 ________ 处
$\text{A.}$ $x=27$
$\text{B.}$ $y=27$
$\text{C.}$ $y=0$
$\text{D.}$ $x=0$
设 $f_1(x)$ 为标准正态分布的概率密度, $f_2(x)$ 为 $[-1,3]$ 上的均匀分布的概率密度, 若 $f(x)=\left\{\begin{array}{l}a f_1(x), x \leq 0 \\ b f_2(x), x>0\end{array}(a>0, b>0)\right.$ 为随机变量的概率密度, 则 $a, b$ 应满足
$\text{A.}$ $2 a+3 b=4$
$\text{B.}$ $3 a+2 b=4$
$\text{C.}$ $a+b=1$
$\text{D.}$ $a+b=2$
填空题 (共 5 题 ),请把答案直接填写在答题纸上
设事件 $A 、 B$ 互不相容, 已知 $P(A)=0.4, P(B)=0.5$, 则 $P(\bar{A} \cdot \bar{B})=$ , 若 $A 、 B$ 独立, 则 $P(A \cup B)=$
设 $X \sim N(1,1)$, 且 $\Phi(1)=0.8413$, 则 $P\{0 < X < 2\}=$ 。
已知二维随机变量 $(X, Y)$ 的联合分布律: 要使 $X 、 Y$ 相互独立, 则 $\alpha, \beta$ 的值为
加油站有两套用来加油的设备, 设备 $A$ 是工作人员操作的, 设备 $B$ 是顾客自己操作的, $A 、 B$ 均装有两根加油软管, 任取一时间, $A 、 B$ 正在使用的软管数分别为 $X 、 Y, X 、 Y$ 的联合分布律为下表,求:
(1) $P(X \leq 1, Y \leq 1)$
(2) 至少有一根软管在使用的概率
(3) $P(X=Y)$
(4) $P\{X+Y=2\}$

设 $A 、 B$ 为两个随机事件, $P\{A\}=0.25, P\{B \mid A\}=0.5, P\{A \mid B\}=0.25$, 令随机变量
$$
X=\left\{\begin{array}{rrr}
1 & A \text { 发生 } \\
0 & A \text { 不发生 }
\end{array} \quad Y=\left\{\begin{array}{rr}
1 & B \text { 发生 } \\
0 & B \text { 不发生 }
\end{array}\right.\right.
$$
(1) 求 $(X, Y)$ 的联合分布律
(2) 求 $P\left\{X^2+Y^2=1\right\}$
解答题 (共 8 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
甲、乙两门高射炮彼此独立地向一架飞机各发一炮, 甲、乙击中飞机的概率分别为 0.3 和 0.4 , 则飞机至少被击中一炮的概率为?
设随机变量 $A$ 为 $x \in(-5,7)$ 上的均匀分布, 则关于 $x$ 的方程 $9 x^2+6 A x+A+6=0$ 有实根的概率为?
仓库中有 10 箱同种规格的产品, 其中 2 箱、 3 箱、 5 箱分别由甲、乙、丙三个厂生产, 三个厂的正品率分别为 $0.7,0.8,0.9$, 现在从这 10 箱产品中任取一箱, 再从中任取一件
(1) 求取出的产品为正品的概率
(2) 如果取出的是正品, 求此件产品由乙厂生产的概率
某保险公司把被保险人分为 3 类: “谨傎的”、“一般的”、“冒失的”, 统计资料表明, 这 3种人在一年内发生事故的概率依次为 $0.05,0.15,0.30$; 如果 “谨慎的” 被保险人占 $20 \%$, “一般的占 $50 \%$, “冒失的” 占 $30 \%$, 问:
(1) 一个被保险人在一年内出事故的概率是多大?
(2) 若已知某被保险人出了事故, 求他是 “谨慎的” 类型的概率。
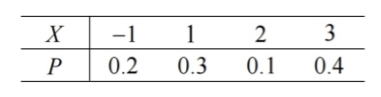
设随机变量 $X$ 的分布律如下: 求: (1) $X$ 的分布函数; (2) $ P\{1 \leq X < 3\} $
设随机变量 $X$ 的概率密度为 $f(x)= \begin{cases}x & 0 \leq x < 1 \\ 2-x & 1 \leq x < 2 \\ 0 & \text { 其他 }\end{cases}$
求: (1) $X$ 的分布函数 $F(x)$
(2) 求 $P\left\{1 < X < \frac{3}{2}\right\}$
设随机变量 $X$ 的概率密度为 $f(x)=\left\{\begin{array}{ll}\frac{x}{2} & 0 < x < A \\ 0 & \text { 其他 }\end{array}\right.$, 求:
(1) 常数 $A$
(2) 分布函数 $F(x)$
(3) $P\left\{-1 < X < \frac{1}{2}\right\}$
设随机变量 $X$ 的概率密度为 $f_x(x)=\left\{\begin{array}{ll}2 e^{-2 x} & x>0 \\ 0 & \text { 其他 }\end{array}\right.$, 若 $Y=1-e^{-2 X}$, 求 $Y$ 的概率密度 $f_Y(y)$ 。