单选题 (共 10 题 ),每题只有一个选项正确
2022 年冬奥会将在我国北京市和张家口市联合举行, 下列历届冬奥会会徽的部分图案中, 是中心对称图形的是
$\text{A.}$  $\text{B.}$
$\text{B.}$  $\text{C.}$
$\text{C.}$  $\text{D.}$
$\text{D.}$ 
下列二次函数中, 其图象的顶点坐标为 $(-3,-1)$ 的是
$\text{A.}$ $y=(x-3)^2+1$
$\text{B.}$ $y=(x+3)^2+1$
$\text{C.}$ $y=(x-3)^2-1$
$\text{D.}$ $y=(x+3)^2-1$
下列事件中, 是必然事件的是
$\text{A.}$ 掷一次骰子, 向上一面的点数是 6
$\text{B.}$ 任意画一个三角形, 其内角和为 $180^{\circ}$
$\text{C.}$ 篮球队员在罚球线上投篮一次, 未投中
$\text{D.}$ 一元二次方程一定有两个实数根
与点 $(2,-3)$ 在同一反比例函数图象上的点是
$\text{A.}$ $(-2,3)$
$\text{B.}$ $(-1,-6)$
$\text{C.}$ $(6,1)$
$\text{D.}$ $(-2,-3)$
如图, $P$ 是等边 $\triangle A B C$ 内部一点, 把 $\triangle A B P$ 绕点 $A$ 逆时针旋转, 使点 $B$ 与点 $C$ 重合, 得到 $\triangle A C Q$,则旋转角的度数是

$\text{A.}$ $70^{\circ}$
$\text{B.}$ $80^{\circ}$
$\text{C.}$ $60^{\circ}$
$\text{D.}$ $50^{\circ}$
方程 $(m-1) x^{|m|+1}-3 x=7$ 是关于 $x$ 的一元二次方程, 则有
$\text{A.}$ $m=1$
$\text{B.}$ $m=-1$
$\text{C.}$ $m= \pm 1$
$\text{D.}$ $m \neq \pm 1$
已知 $\triangle A B C$ 与 $\triangle A^{\prime} B^{\prime} C^{\prime}$ 相似, 点 $A$ 与 $A^{\prime}$, 点 $B$ 与 $B^{\prime}$ 对应, 若 $\frac{C_{\triangle A B C}}{C_{\triangle A^{\prime} B^{\prime} C^{\prime}}}=\frac{1}{4}$, 且 $\triangle A B C$ 的中线 $A D$ 的长为 5 , 则 $A D$ 的对应中线 $A^{\prime} D^{\prime}$ 的长为
$\text{A.}$ 10
$\text{B.}$ 20
$\text{C.}$ 80
$\text{D.}$ $\frac{5}{4}$
如图, $P A 、 P B$ 分别与 $\odot O$ 相切于 $A 、 B$ 两点, $C$ 是圆上一点, 连接 $A C 、 B C$, 若 $\angle A C B=62^{\circ}$, 则 $\angle P$ 的度数为

$\text{A.}$ $56^{\circ}$
$\text{B.}$ $62^{\circ}$
$\text{C.}$ $66^{\circ}$
$\text{D.}$ $68^{\circ}$
将三角形纸片 $\triangle A B C$ 按如图所示的方式折蛋, 使点 $B$ 落在边 $A C$ 上, 记为点 $B^{\prime}$, 折痕为 $E F$. 已知 $A B=A C=6, B C=8$, 若 $\triangle F B^{\prime} C \sim \triangle A B C$, 那么 $B F$ 的长度是

$\text{A.}$ $\frac{24}{7}$
$\text{B.}$ 4
$\text{C.}$ $\frac{12}{7}$
$\text{D.}$ 2
二次函数 $y=a x^2+b x+c(a \neq 0)$ 的部分图象如图所示, 图象过点 $(-1,0)$, 对称轴为直线 $x$ $=2$, 下列结论: (1) $4 a+b=0$ ;(2) $8 a+7 b+2 c>0$ ;(3)若方程 $a(x+1) \quad(x-5)=-3$ 的两根为 $x_1$ 和 $x_2$, 且 $x_1 < x_2$, 则 $x_1 < -1 < 5 < x_2$; (4) $\frac{4 a}{b}+\frac{b}{a}=-4$, 其中正确的结论有

$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
填空题 (共 5 题 ),请把答案直接填写在答题纸上
如图, 直线 $A D / / B E / / C F, B C=\frac{1}{2} A B, D E=4$, 那么 $E F$ 的值是

二次函数 $y=-2(x-4)^2+8$ 的最大值为
某种商品原价每件售价为 400 元, 经过连续两次降价后, 每件售价为 288 元, 设平均每次降价的百分率为 $x$, 则可列方程为
如图, Rt $\triangle A B C$ 的内切圆 $\odot O$ 与两直角边 $A B 、 B C$ 分别相切于点 $D 、 E$, 过劣弧 $D E$ (不包括端点 $D 、 E)$ 上任一点 $P$ 作 $\odot O$ 的切线 $M N$, 与 $A B 、 B C$ 分别交于点 $M 、 N, A B=8, B C=6$, 则 Rt $\triangle M B N$ 的周长

如图, 反比例函数 $y=\frac{3}{x}$ 的图象上有一动点 $A$, 连接 $A O$ 并延长交图象的另一支于点 $B$, 在第二象限内有一点 $C$, 满足 $A C=B C$, 当点 $A$ 运动时, 点 $C$ 始终在函数 $y=\frac{k}{x}$ 的图象上运动, $\tan \angle C A B=$ 2 , 则 $k=$

解答题 (共 9 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
(1)解方程: $x^2-2 x-3=0$ ;
(2)计算: $4 \sin 60^{\circ} \cos 30^{\circ}-\tan 45^{\circ}$.
如图, 已知 $A(-4,2), B(-2,6), C(0,4)$ 是直角坐标系平面上三点.
(1) 以原点 $O$ 为位似中心, 在第四象限内画出将 $\triangle A B C$ 缩小为原来的一半后的 $\triangle A_1 B_1 C$ 1 i
( 2 ) 画出 $\triangle A B C$ 绕点 $C$ 顺时针旋转 $90^{\circ}$ 后的 $\triangle A_2 B_2 C_2$, 并求出线段 $B C$ 所扫过的图形面积.

“圆材埋壁” 是我国古代著名数学著作《九章算术》中的问题: “今有圆材, 埋在壁中, 不知大小,以锯锯之, 深一寸, 锯道长一尺, 问径几何? ”用现在的数学语言可表达为: “如图, $C D$ 为 $\odot O$ 的直径, 弦 $A B \perp C$ $D$ 于点 $E, C E=1$ 寸, $A B=10$ 寸, 则直径 $C D$ 的长为多少?

北京将于 2022 年举办冬奥会和冬残奥会, 中国将成为一个举办过五次各类奥林匹克运动会的国家小亮是个集邮爱好者, 他收集了如图所示的四张纪念邮票(除正面内容不同外, 其余均相同 ), 现将四张邮票背面朝上, 洗匀放好.
(1)小亮从中随机抽取一张邮票是“冬残奥会吉祥物雪容融”的概率是
(2)小亮从中随机抽取一张邮票 (不放回), 再从余下的邮票中随机抽取一张, 请你用列表或画树状图的方法求抽到的两张邮票恰好是“冬奥会会徽”和“冬奥会吉祥物冰墩墩”的概率。( 这四张邮票依次分别用字母 $A, B, C, D$ 表示)

一次函数 $y=k x+b$ 的图象与反比例函数 $y=\frac{m}{x}$ 的图象相交于 $A(-1,4) 、 B(-4, n)$.
(1) 求反比例函数与一次函数的解析式;
(2) 求 $\triangle O A B$ 的面积;
(3) 直接写出不等式 $\frac{m}{x}>k x+b$ 的解集.

由我国完全自主设计与建造的首艘国产航母山东舰于 2019 年 12 月 17 日交付海军. 如图, 某日山东舰在南海海域开展训练时在 $A$ 处测得小岛 $C$ 在该舰的北偏东 $60^{\circ}$ 方向, 往东行驶 20 海里后到达 $B$ 处, 此时测得小岛 $C$ 在该舰的北偏东 $30^{\circ}$ 方向, 已知以小岛为 $C$ 中心, 周围 10 海里内有暗礁, 问航母山东舰继续向东航行是否有触礁的危险?

如图, 已知在 $\triangle A B C$ 中, $A D$ 是 $\triangle A B C$ 的中线, $\angle D A C=\angle B$, 点 $E$ 在边 $A D$ 上, $C E=C D$.
(1) 求证: $\triangle A C E \sim \triangle B A D$;
(2) 求证: $A C^2=2 A E \cdot A D$.

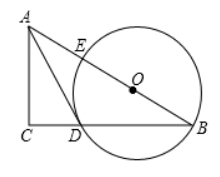
如图所示, 在 $R t \triangle A B C$ 中, 点 $O$ 在斜边 $A B$ 上, 以 $O$ 为圆心, $O B$ 为半径作圆 $O$, 分别与 $B C 、 A B$相交于点 $D 、 E$, 连接 $A D$, 已知 $\angle C A D=\angle B$;
(1) 求证: $A D$ 是 $\odot O$ 的切线;
(2) 若 $\angle B=30^{\circ}, C D=\frac{3}{2}$, 求劣弧 $B D$ 的长;
(3) 若 $A C=2, B D=3$, 求 $A E$ 的长.
平面直角坐标系中, 已知抛物线的顶点为 $A(2,4)$, 且经过坐标原点.
(1) 求抛物线的函数解析式;
(2) 如图1, 设抛物线与 $x$ 轴的另一交点为 $B$, 点 $C$ 为抛物线上 $A, B$ 之间一点, 连接 $O A, O C$, 若 $\angle A O C=\angle A O y$, 求点 $C$ 的坐标;
( 3 ) 如图 2 , 若直线 $y=k x-2 k+5$ 与抛物线交于 $M, N$ 两点, 点 $N$ 关于抛物线对称轴的对称点为 $P$, 当 $k < 0$ 时, 试说明直线 $M P$ 过一定点 $Q$, 并求出点 $Q$ 的坐标.
