单选题 (共 7 题 ),每题只有一个选项正确
关于洛伦兹力的应用,下列说法正确的是
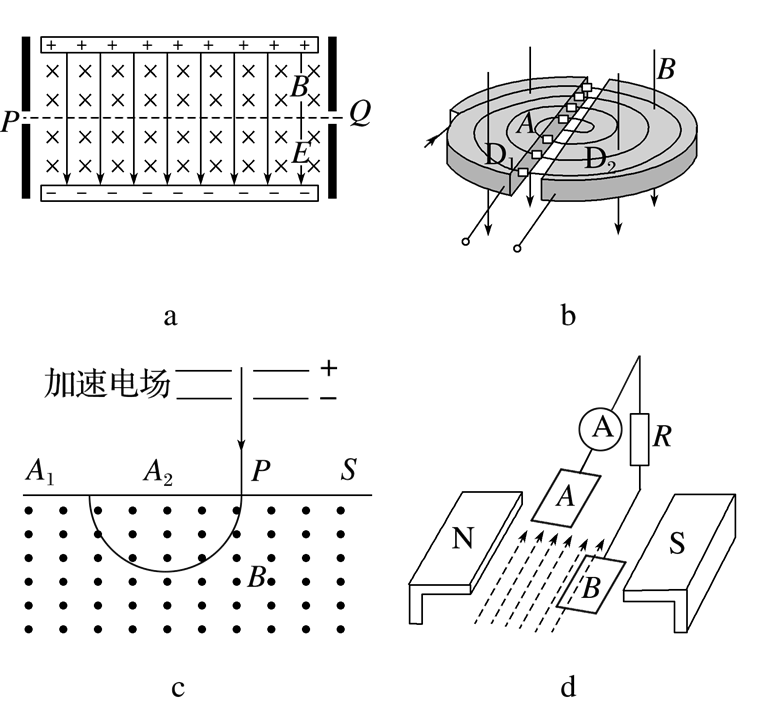
$\text{A.}$ 图a速度选择器中筛选出的粒子沿着 $P Q$ 做匀加速直线运动
$\text{B.}$ 图 b 回旋加速器接入的工作电源是直流电
$\text{C.}$ 图 c 是质谱仪的主要原理图,其中 1 H 、 ${ }_1^2 H 、{ }_1^3 H$ 在磁场中偏转半径最大的是 ${ }_1^3 H$
$\text{D.}$ 图 d 是磁流体发电机,将一束等离子体喷入磁场,$A 、 B$ 两板间会产生电压,且 $A$ 板电势高
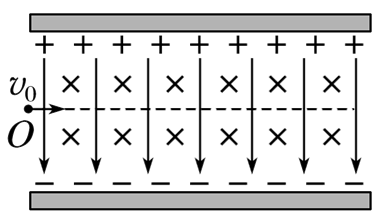
一对平行金属板中存在匀强电场和匀强磁场,其中电场的方向与金属板垂直,磁场的方向与金属板平行且垂直纸面向里,如图所示.一质子 $( lH )$ 以速度 $v_0$ 自 $O$ 点沿中轴线射入,恰沿中轴线做匀速直线运动.下列粒子分别自 $O$ 点沿中轴线射入,能够做匀速直线运动的是(所有粒子均不考虑重力的影响)
$\text{A.}$ 以速度 $\frac{v_0}{2}$ 射入的正电子 $( i e )$
$\text{B.}$ 以速度 $v_0$ 射入的电子 $(-1 e )$
$\text{C.}$ 以速度 $2 v_0$ 射入的核 $\left({ }_1^2 H \right)$
$\text{D.}$ 以速度 $4 v_0$ 射入的 $\alpha$ 粒子 $\left({ }_2^4 He \right)$
自行车速度计可以利用霍尔效应传感器获知自行车轮的运动速率.如图甲所示,一块磁体安装在前轮上,轮子每转一圈,磁体就靠近传感器一次,传感器就会输出一个脉冲电压.如图乙所示,电源输出电压为U1,当磁场靠近霍尔元件时,在导体前后表面间出现电势差U2(前表面的电势低于后表面的电势).下列说法中错误的是

$\text{A.}$ 图乙中霍尔元件的载流子带负电
$\text{B.}$ 已知自行车车轮的半径,再根据单位时间内的脉冲数,即获得车速大小
$\text{C.}$ 若传感器的电源输出电压U1变大,则U2变大
$\text{D.}$ 若自行车的车速越大,则U2越大
如图所示,电荷量相等的两种离子氖20和氖22先后从容器A下方的狭缝S1飘入(初速度为零)电场区,经电场加速后通过狭缝S2、S3垂直于磁场边界MN射入匀强磁场,磁场方向垂直纸面向里,离子经磁场偏转后轨迹发生分离,最终到达照相底片D上.不考虑离子间的相互作用,则
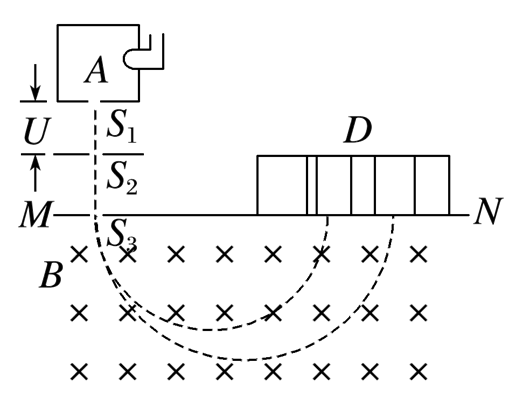
$\text{A.}$ 静电力对每个氖20和氖22做的功不相等
$\text{B.}$ 氖22进入磁场时的速度较大
$\text{C.}$ 氖22在磁场中运动的半径较小
$\text{D.}$ 若加速电压发生波动,两种离子打在照相底片上的位置可能重叠
在实验室中有一种污水流量计如图甲所示,其原理可以简化为如图乙所示模型:废液内含有大量正、负离子,从直径为 $d$ 的圆柱形容器右侧流入,左侧流出.流量 $Q$ 等于单位时间通过横截面的导电液体的体积.空间有垂直纸面向里且磁感应强度大小为 $B$ 的匀强磁场,并测出 $M$ 、 $N$ 间的电压 $U$ ,则下列说法正确的是
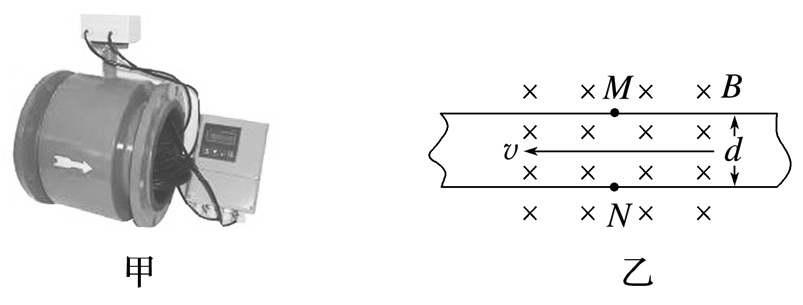
$\text{A.}$ 正、负离子所受洛伦兹力方向是相同的
$\text{B.}$ 容器内液体的流速为 $v=\frac{U}{B d}$
$\text{C.}$ 污水流量计也可以用于测量不带电的液体的流速
$\text{D.}$ 污水流量为 $Q=\frac{\pi U d}{2 B}$
如图为一种改进后的回旋加速器示意图,其中盒缝间的加速电场场强大小恒定,且被限制在AC板间,虚线中间不需加电场,带电粒子从P0处以速度v0沿电场线方向射入加速电场,经加速后再进入D形盒中做匀速圆周运动,对这种改进后的回旋加速器,下列说法正确的是

$\text{A.}$ 加速粒子的最大速度与D形盒的尺寸无关
$\text{B.}$ 带电粒子每运动一周被加速一次
$\text{C.}$ 带电粒子每运动一周P1P2等于P2P3
$\text{D.}$ 加速电场方向需要做周期性的变化
现代质谱仪可用来分析比质子重很多倍的离子,其示意图如图所示,其中加速电压恒定.质子在入口处从静止开始被加速电场加速,经匀强磁场偏转后从出口离开磁场.若某种一价正离子在入口处从静止开始被同一加速电场加速,为使它经匀强磁场偏转后仍从同一出口离开磁场,需将磁感应强度增加到原来的12倍.此离子和质子的质量比约为

$\text{A.}$ 11
$\text{B.}$ 12
$\text{C.}$ 121
$\text{D.}$ 144
多选题 (共 1 题 ),每题有多个选项正确
图甲是回旋加速器的示意图,其核心部分是两个D形金属盒,在加速带电粒子时,两金属盒置于匀强磁场中,并与高频电源相连.带电粒子从静止开始运动的速率v随时间t变化如图乙,已知tn时刻粒子恰射出回旋加速器,不考虑相对论效应、粒子所受的重力和穿过狭缝的时间,下列判断正确的是
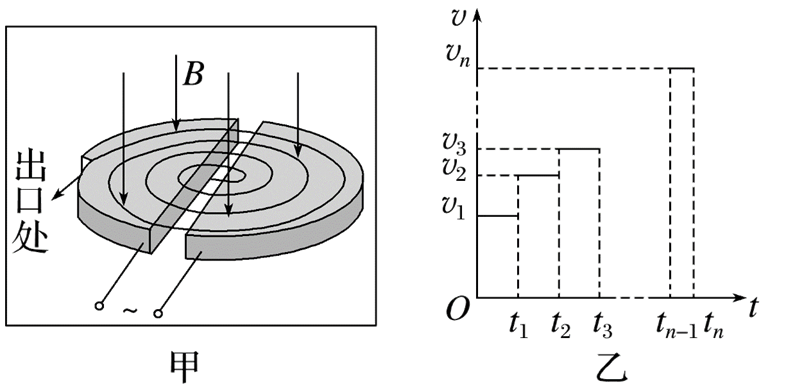
$\text{A.}$ $t_3-t_2=t_2-t_1=t_1$
$\text{B.}$ $v_1: v_2: v_3=1: 2: 3$
$\text{C.}$ 粒子在电场中的加速次数为 $\frac{v_n^2}{v_1^2}$
$\text{D.}$ 同一D形盒中粒子的相邻轨迹半径之差保持不变
解答题 (共 1 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
如图为某种质谱仪的示意图,该质谱仪由加速电场、静电分析器和磁分析器组成.静电分析器通道中心轴线的半径为R,通道内存在均匀辐向电场;磁分析器有范围足够大的有界匀强磁场,方向垂直纸面向外.质子和待测未知粒子x先后从静止开始经加速电压为U的电场加速后沿中心轴线通过静电分析器,从P点垂直边界进入磁分析器,最终分别打到胶片上的C、D点.已知质子质量为m、电荷量为q,粒子x的电荷量是质子的2倍,PC=2R,PD= $2\sqrt{2}$ .求:
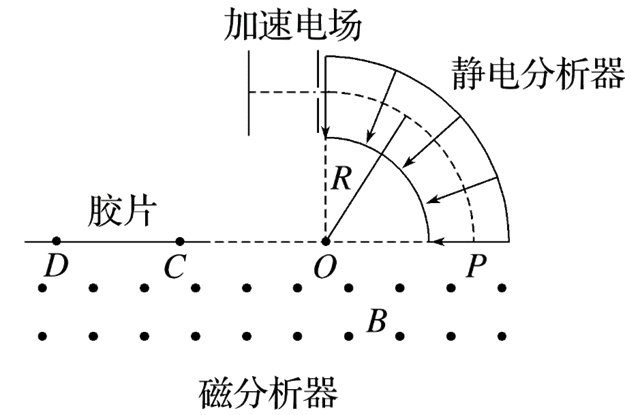
(1)静电分析器中心轴线处的电场强度大小E;
(2)磁感应强度大小B;
(3)粒子x的质量M.