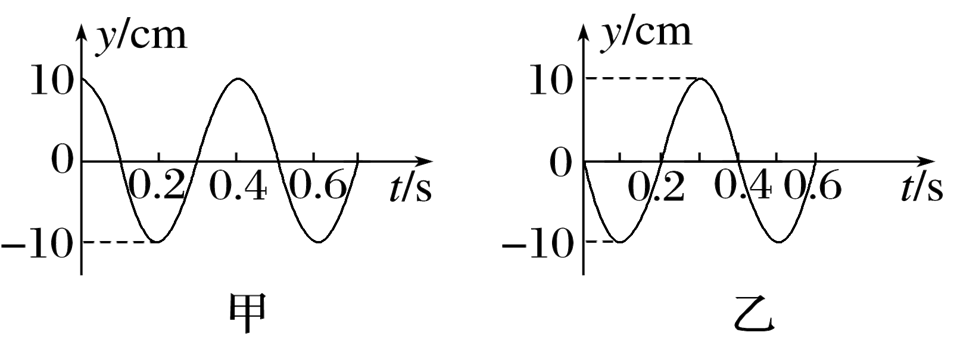单选题 (共 8 题 ),每题只有一个选项正确
超声波是一种频率高于20 000 Hz 的声波,波长很短,广泛应用于生活与生产实践.关于超声波及应用,下列说法正确的是
$\text{A.}$ 在同种介质中,超声波的速度大于次声波的速度
$\text{B.}$ 超声波的频率越高,衍射本领越强
$\text{C.}$ 高速公路上的测速仪发出超声波波长大于所接收波的波长,说明此时车正在靠近测速仪
$\text{D.}$ “彩超”检查身体时,超声波迎着血液流动方向发射,仪器接收到的反射回来的波的频率低于其发射的超声波的频率
A、B为同一波源发出的两列波,某时刻在不同介质、相同距离上的波形如图所示,则两列波的波速大小之比vA∶vB是
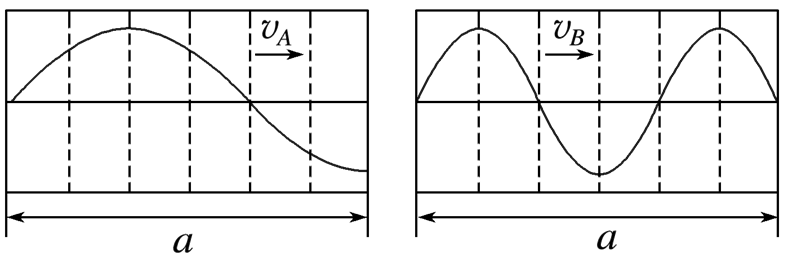
$\text{A.}$ 1∶3
$\text{B.}$ 1∶2
$\text{C.}$ 2∶1
$\text{D.}$ 3∶1
一列简谐横波沿x轴正方向传播,某时刻的波形如图所示,关于质点P的说法正确的是

$\text{A.}$ 该时刻速度沿 $y$ 轴正方向
$\text{B.}$ 该时刻加速度沿 $y$ 轴正方向
$\text{C.}$ 此后 $\frac{1}{4}$ 周期内通过的路程为 $A$
$\text{D.}$ 此后 $\frac{1}{2}$ 周期内沿 $x$ 轴正方向迁移为 $\frac{1}{2} \lambda$
两辆汽车甲与乙,在t=0时刻,分别距十字路O处的距离为x甲和x乙.两车分别以速率v甲和v乙沿水平的、相互正交的公路匀速前进,如图所示.汽车甲持续地以固定的频率f0鸣笛,则在任意时刻t汽车乙的司机所检测到的笛声频率将如何变化(已知声速为u,且有u>v甲、u>v乙)
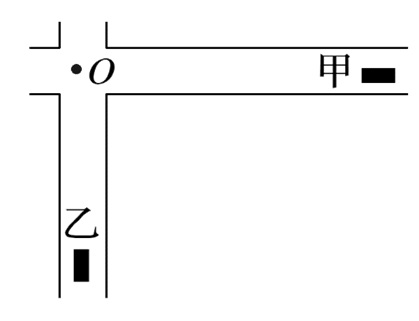
$\text{A.}$ 当两车均向O运动(在到达O之前)时,汽车乙的司机接收到的频率一定比波源发出的频率低
$\text{B.}$ 当两车均向O运动(在到达O之前)时,汽车乙的司机接收到的频率可能等于波源发出的频率
$\text{C.}$ 当两车均向远离O的方向运动时,汽车乙的司机接收到的频率一定比波源发出的频率低
$\text{D.}$ 当两车均向远离O的方向运动时,汽车乙的司机接收到的频率一定比波源发出的频率高
$\text{A.}$ 质点A位于振动加强区
$\text{B.}$ 质点A比质点B振动得快
$\text{C.}$ 0~4 s内,质点A的最小位移为-2 m
$\text{D.}$ 0~4 s内,质点B的最大位移为2 m
一列简谐横波在t=1/3 s时的波形图如图甲所示,P、Q是介质中的两个质点,图乙是质点Q的振动图像.关于该简谐波下列说法中正确的是
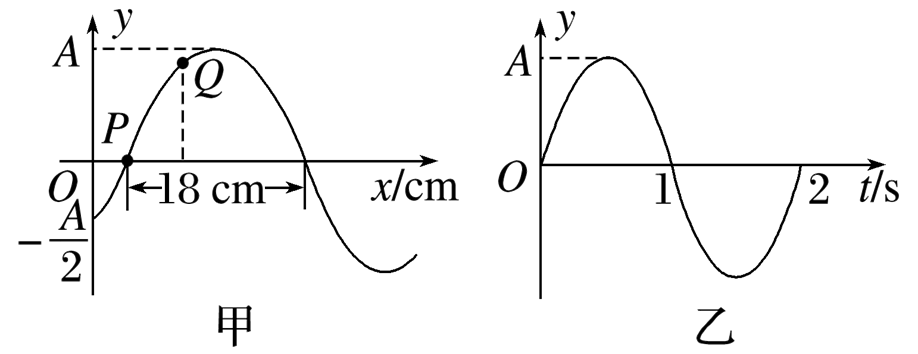
$\text{A.}$ 波速为 $9 cm / s$
$\text{B.}$ 沿 $x$ 轴正方向传播
$\text{C.}$ 质点 $Q$ 的平衡位置坐标 $x=9 cm$
$\text{D.}$ 在 $t=\frac{1}{2} s$ 时质点 $P$ 移动到 $O$ 点
一列简谐横波在均匀介质中沿 $x$ 轴负方向传播,已知 $x=\frac{5}{4} \lambda$ 处质点的振动方程为 $y=A \cos \left(\frac{2 \pi}{T} t\right)$ ,则 $t=\frac{3}{4} T$ 时刻的波形图正确的是
$\text{A.}$ 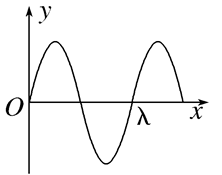 $\text{B.}$
$\text{B.}$ 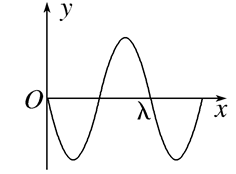 $\text{C.}$
$\text{C.}$ 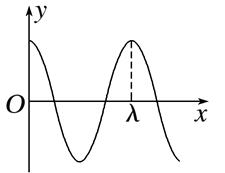 $\text{D.}$
$\text{D.}$ 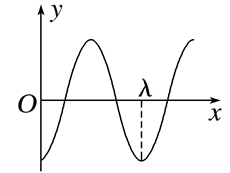
如图所示,一列振幅为10 cm的简谐横波,其传播方向上有两个质点P和Q,两者的平衡位置相距3 m.某时刻两质点均在平衡位置且二者之间只有一个波谷,再经过0.3 s,Q第一次到达波峰.则下列说法正确的是

$\text{A.}$ 波长可能为2 m
$\text{B.}$ 周期可能为0.24 s
$\text{C.}$ 波速可能为15 m/s
$\text{D.}$ 0.3 s内质点P的位移大小为10 cm
多选题 (共 2 题 ),每题有多个选项正确
如图所示,蟾蜍在池塘边平静的水面上鸣叫,形成了水波.已知水波的传播速度与水的深度成正相关,蟾蜍的鸣叫频率f=1 451 Hz.下列说法正确的是

$\text{A.}$ 水波从浅水区传入深水区,频率变大
$\text{B.}$ 在深水区,水波更容易发生衍射现象
$\text{C.}$ 池塘水面上的落叶会被水波推向岸边
$\text{D.}$ 若水波两个相邻波峰间距离为0.5 cm,则此处水波的波速约为7.3 m/s
两列振幅相等、波长均为λ、周期均为T的简谐横波沿同一绳子相向传播,若两列波均由一次全振动产生,t=0时刻的波形如图所示,此时两列波相距λ,则
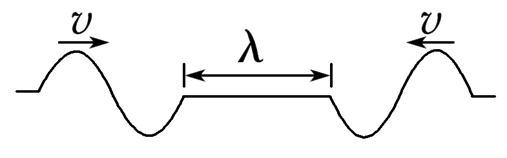

$\text{A.}$ $t=\frac{T}{4}$ 时,波形如图甲所示
$\text{B.}$ $t=\frac{T}{2}$ 时,波形如图乙所示
$\text{C.}$ $t=\frac{3 T}{4}$ 时,波形如图丙所示
$\text{D.}$ $\delta=T$ 时,波形如图丁所示
解答题 (共 2 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
两列简谐横波分别沿x轴正方向和负方向传播,两波源分别位于x轴上-0.2 m和1.2 m处,两波的波速均为0.4 m/s,波源的振幅均为2 cm.如图为t=0时刻两列波的图像,此刻平衡位置在x轴上0.2 m和0.8 m的P、Q两质点开始振动.质点M、N的平衡位置分别处于x轴上0.5 m和0.6 m 处.求:

(1)M点开始振动的时刻;
(2)0~3.0 s内质点N运动的路程.
在一列沿水平直线传播的简谐横波上有相距4 m的A、B两点,如图甲、乙分别是A、B两质点的振动图像.已知该波波长大于2 m,求这列波可能的波速.