解答题 (共 9 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知平行四边形 $A B C D$ 的对角线 $\overrightarrow{A C}= \alpha , \overrightarrow{B D}= \beta$ ,求 $\overrightarrow{A B}, \overrightarrow{B C}$ .
判断下列等式何时成立:
(1)$| \alpha + \beta |=| \alpha - \beta |$ ,
(2)$| \alpha + \beta |=| \alpha |+| \beta |$ ,
(3)$| \alpha + \beta |=| \alpha |-| \beta |$ ,
(4)$\frac{ \alpha }{| \alpha |}=\frac{ \beta }{| \beta |}$ .
已知 $\alpha =(3,5,4), \beta =(-6,1,2), \gamma =(0,-3,-4)$ ,求 $2 \alpha +3 \beta$ $+4 \gamma$ .
已知点 $A(3,5,7)$ 和点 $B(0,1,-1)$ ,求向量 $A B$ ,并求 $A$ 关于 $B$的对称点 $C$ 的坐标.
判断下列向量中哪些是共线的.
$$
\begin{gathered}
\alpha _1=(1,2,3), \alpha _2=(1,-2,3), \alpha _3=(1,0,2), \alpha _4=(-3,6,-9), \\
\alpha _5=(2,0,4), \alpha _6=(-1,-2,-3), \alpha _7=\left(\frac{1}{4}, \frac{2}{4}, \frac{3}{4}\right), \alpha _8=\left(\frac{1}{2},-1,-\frac{3}{2}\right) .
\end{gathered}
$$
设 $\alpha , \beta , \gamma$ 均为非零向量,其中任意两个向量不共线,但 $\alpha + \beta$与 $\gamma$ 共线, $\beta + \gamma$ 与 $\alpha$ 共线,试证 $\alpha + \beta + \gamma = 0$ 。
判断 $\alpha , \beta , \gamma$ 是否共面.
(1) $\alpha =(4,0,2), \beta =(6,-9,8), \gamma =(6,-3,3)$ ;
(2) $\alpha =(1,-2,3), \beta =(3,3,1), \gamma =(1,7,-5)$ .
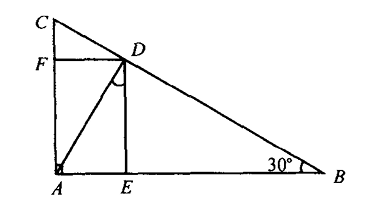
如图 ,在三角形 $\triangle A B C$ 中,$\angle A=90^{\circ}, \angle B=30^{\circ}, A D$ 是 $B C$ $\rightarrow \rightarrow$边上的高,求点 $D$ 在坐标系 $\{A: \overrightarrow{A B}, \overrightarrow{A C}\}$ 下的坐标.
用定义证明矩阵线性空间 $M _{2 \times 2}( R )$ 中四个元素:
$$
E _{11}=\left[\begin{array}{ll}
1 & 0 \\
0 & 0
\end{array}\right], E _{12}=\left[\begin{array}{ll}
0 & 1 \\
0 & 0
\end{array}\right], E _{21}=\left[\begin{array}{ll}
0 & 0 \\
1 & 0
\end{array}\right], E _{22}=\left[\begin{array}{ll}
0 & 0 \\
0 & 1
\end{array}\right]
$$
线性无关。