单选题 (共 8 题 ),每题只有一个选项正确
已知椭圆 $\frac{ x ^2}{ 2 5 }+\frac{ y ^2}{16}= 1$ 上一点 $P$ 到椭圆的一个焦点的距离为 3 ,则 $P$ 到另一个焦点的距离为()
$\text{A.}$ 7
$\text{B.}$ 5
$\text{C.}$ 3
$\text{D.}$ 2
已知直线 $l$ 过点 $P ( 3 4 )$ ,它的倾斜角是直线 $y = x + 1$ 的两倍,则直线 $l$ 的方程为()
$\text{A.}$ $y-4=0$
$\text{B.}$ $x-3=0$
$\text{C.}$ $y-4=2(x-3)$
$\text{D.}$ $y-4=x-3$
双曲线 $x ^{ 2 }- y ^{ 2 }=1$ 的渐近线方程是( )
$\text{A.}$ $y= \pm 2 x$
$\text{B.}$ $y= \pm \sqrt{2} x$
$\text{C.}$ $y = \pm x$
$\text{D.}$ $y= \pm \frac{1}{2} x$
方程 $x ^{ 2 }+ y ^{ 2 }+ 4 x - 2 y + 5 m = 0$ 表示圆的条件是
$\text{A.}$ $\frac{1}{4} < m < 1$
$\text{B.}$ $m>1$
$\text{C.}$ $m < \frac{1}{4}$
$\text{D.}$ $m < 1$
若椭圆的两个焦点将长轴三等分,则它的离心率是
$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ $\frac{1}{3}$
$\text{C.}$ $\frac{1}{4}$
$\text{D.}$ $\frac{1}{6}$
直线 $x+2 y+1=0$ 被圆 $(x-2)^2+(y-1)^2=25$ 所截得的弦长等于( )
$\text{A.}$ $2 \sqrt{5}$
$\text{B.}$ $3 \sqrt{5}$
$\text{C.}$ $4 \sqrt{5}$
$\text{D.}$ $5 \sqrt{5}$
$M$ 为抛物线 $y ^2= 4 x$ 上一动点, $F$ 为拖物线焦点,定点 $P (3,1)$ ,则 $| M P |+| M F |$ 的最小值为( )
$\text{A.}$ 3
$\text{B.}$ 4
$\text{C.}$ 5
$\text{D.}$ 6
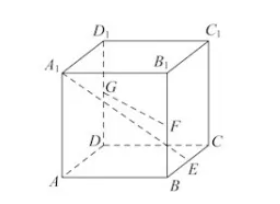
在棱长为 4 的正方体 $A B C D - A _1 B _1 C _{ 1 } D _1$ 中, $E , F , G$ 分别是棱 $B C , B B_{ b } D D_1$ 的中点,过 $F G$ 作平面 $\alpha$ ,使得 $A _{ 1 } E / / \alpha$ ,则点 A 到平面 $\alpha$ 的距离是
$\text{A.}$ $\frac{2 \sqrt{17}}{17}$
$\text{B.}$ $\frac{6 \sqrt{17}}{17}$
$\text{C.}$ $\frac{10 \sqrt{17}}{17}$
$\text{D.}$ $\frac{14 \sqrt{17}}{17}$
多选题 (共 3 题 ),每题有多个选项正确
已知拋物线 $C$ 的焦点在直线 $2 x - y + 4 = 0$ 上,则扰物线 $C$ 的标准方程为()
$\text{A.}$ $y^2=8 x$
$\text{B.}$ $y^2=-8 x$
$\text{C.}$ $x^2=16 y$
$\text{D.}$ $x^2=-16 y$
已知圆 $C :( x - a )^{ 2 }+( y - 1 )^{ 2 }= 4 a$ 的半径为 2 ,则( )
$\text{A.}$ $a=1$
$\text{B.}$ 点 $( 1 , 4 )$ 在圆 $C$ 的外部
$\text{C.}$ 圆 $(x-9)^2+(y+5)^2=64$ 与圆 $C$ 外切
$\text{D.}$ 当直线 $m x + y - 2 = 0$ 平分圆 $C$ 的周长时, $m =-1$
已知椭圆 $C: \frac{x^2}{25}+\frac{y^2}{9}=1, F_1, F_2$ 分别为它的左右焦点,点 $A, B$ 分别为它的左右顶点,已知定点 $Q (4,2)$ ,点 $P$ 是椭圆上的一个动点,下列结论中正确的有( )
$\text{A.}$ 存在点 $P$ ,使得 $\angle K_1 P F_2=120^{\circ}$
$\text{B.}$ 直线 $P A$ 与直线 $P B$ 斜率乘积为定值
$\text{C.}$ $\frac{1}{\left|P F_1\right|}+\frac{25}{\left|P F_2\right|}$ 有最小值 $\frac{18}{5}$
$\text{D.}$ $|P Q|+\left|P K_{ 1 }\right|$ 的范围为 $[ 2 \sqrt{17}, 1 2 ]$
填空题 (共 3 题 ),请把答案直接填写在答题纸上
过两点 $(-1,1)$ 和 $(3,9)$ 的直线在 $x$ 轴上的截距是
如果直线 $a x+2 y+2=0$ 与直线 $3 x-y-2=0$ 平行,则 $a$ 的值为
已知抛物线 $y ^{ 2 }=8 x$ ,准线为 $l$ ,过 $( 2 , 0)$ 的直线交拖物线于 $A, B$ 两点,过 $A$ 作 $A P \perp l$ 于点 $P$ ,则 $| A B |+| A P |$ 的最小值为
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知向量 $\overrightarrow{ a }=( 1 , 3 ,- 2 ), \overrightarrow{ b }=( 1 , 0 , 2 ), \overrightarrow{ c }=( m , n ,- 4 )$ .
(1)若 $\overrightarrow{ a } / / \overrightarrow{ c }$ ,求 $|\vec{b}+\overrightarrow{ c }|$ 的值;
(2)若 $\overrightarrow{ b } \perp \overrightarrow{ c },|\overrightarrow{ c }|= 9$ ,求 $\overrightarrow{ a } \cdot \overrightarrow{ c }$ 值
已知双曲线 $C$ 的方程为 $\frac{ x ^2}{ a ^2}-\frac{ y ^2}{ b ^{ 2 }}= 1 ( a > 0 , b > 0 )$ ,实轴长和离心率均为 2 .
(1)求双曲线 $C$ 的标准方程;
(2)过 $E (0,2)$ 且倾斜角为 $4 5$ 的直线 $l$ 与双曲线 $C$ 交于 $M , N$ 两点,求 $\overrightarrow{ O M } \cdot \overrightarrow{O N}$ 的值.( $O$ 为坐标原点)
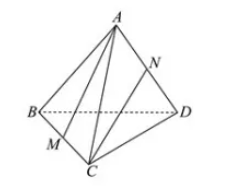
如图,在三㮦锥 $A - B C D$ 中,已知 $M , N$ 分别为棱 $B C , A D$ 的中点.
(1)设 $\overrightarrow{ C A }=\overrightarrow{ a }, \overrightarrow{ C B }=\overrightarrow{ b }, \overrightarrow{ C D }=\overrightarrow{ c }$ ,试用向量 $\overrightarrow{ a }, \overrightarrow{ b }, \overrightarrow{ c }$ 表示 $\overrightarrow{ M A }$ 和 $\overrightarrow{ C N }$ ;
(2)若三棱锥 $A - B C D$ 各条棱长均为 2 ,求直线 $A M$ 和 $C N$ 夹角的余弦值.
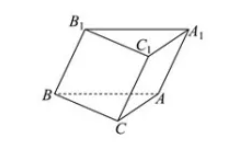
如图,斜三棱柱 $A B C - A _{ 1 } B _1 C _{ 1 }$ 的底面是直角三角形,$\angle A C B= 9 0 ^ { * }$ ,点 $B _{ 1 }$ 在底面 $A B C$ 内的射影㣛好是 $B C$ 的中点,且 $B C = C A = 2$ .
(1)求证:平面 $A C C_1 A_1 \perp$ 平面 $B_1 C_1 C B$ ;
(2)若斜棱柱的高为 $\sqrt{3}$ ,求平面 $A$ RB ${ }_1$ 与平面 $A B_1 C_1$ 夹角的余弦值.
已知 $M (1, t)$ 是抛物线 $C : y ^{ 2 }= 2 p x ( p > 0 )$ 上一点, $F$ 是 $C$ 的焦点,$| F M |= 2$ .
(1)求 $C$ 的方程及 $M$ 的坐标;
(2)设 $N (- 1 , 0)$ ,直线 $l$ 与 $C$ 交于 $A, B$ 两点,若 $\triangle N A B$ 的重心在 $C$ 上,求 $\triangle N A B$ 面积的最大值.