单选题 (共 10 题 ),每题只有一个选项正确
计算 $\sqrt{2} \times \sqrt{7}$ 的结果是
$\text{A.}$ $2 \sqrt{7}$
$\text{B.}$ $7 \sqrt{2}$
$\text{C.}$ 14
$\text{D.}$ $\sqrt{14}$
计算 $\sqrt{9^2-6^2}$ 所得结果是
$\text{A.}$ 3
$\text{B.}$ $\sqrt{6}$
$\text{C.}$ $3 \sqrt{5}$
$\text{D.}$ $\pm 3 \sqrt{5}$
式子 $\sqrt{x}$ 在实数范围内有意义,则 $x$ 的取值范围是
$\text{A.}$ $x>0$
$\text{B.}$ $x \geq 0$
$\text{C.}$ $x < 0$
$\text{D.}$ $x \leq 0$
若式子 $\sqrt{2 m-3}$ 有意义,则 $m$ 的取值范围是
$\text{A.}$ $m \leq \frac{2}{3}$
$\text{B.}$ $m \geq-\frac{3}{2}$
$\text{C.}$ $m \geq \frac{3}{2}$
$\text{D.}$ $m \leq-\frac{2}{3}$
已知 $1 < x < 2$ ,化简 $\sqrt{(x-1)^2}+|x-2|$ 的结果为
$\text{A.}$ -1
$\text{B.}$ 1
$\text{C.}$ $2 x-3$
$\text{D.}$ $3-2 x$
已知 $m=\sqrt{27}-\sqrt{3}$ ,则实数 $m$ 的范围是()
$\text{A.}$ $2 < m < 3$
$\text{B.}$ $3 < m < 4$
$\text{C.}$ $4 < m < 5$
$\text{D.}$ $5 < m < 6$
矩形相邻两边长分别为 $\sqrt{2} cm, ~ \sqrt{5} cm$ ,设其面积为 $S cm^2$ ,则 $S$ 在哪两个连续整数之间()
$\text{A.}$ 1 和 2
$\text{B.}$ 2 和 3
$\text{C.}$ 3 和 4
$\text{D.}$ 4 和 5
下列计算正确的是( )
$\text{A.}$ $a^3+a^5=a^6$
$\text{B.}$ $a^6 \div a^3=a^2$
$\text{C.}$ $(-a)^2=a^2$
$\text{D.}$ $\sqrt{a^2}=a$
估计 $\sqrt{12}(\sqrt{2}+\sqrt{3})$ 的值应在
$\text{A.}$ 8 和 9 之间
$\text{B.}$ 9 和 10 之间
$\text{C.}$ 10 和 11 之间
$\text{D.}$ 11 和 12 之间
将一组数 $\sqrt{2}, 2, \sqrt{6}, 2 \sqrt{2}, \sqrt{10}, 2 \sqrt{3},...$ ,按以下方式进行排列:
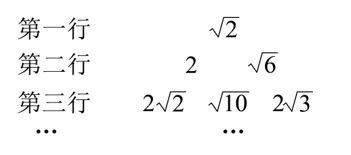
则第八行左起第 1 个数是( )
$\text{A.}$ $7 \sqrt{2}$
$\text{B.}$ $8 \sqrt{2}$
$\text{C.}$ $\sqrt{58}$
$\text{D.}$ $4 \sqrt{7}$
填空题 (共 9 题 ),请把答案直接填写在答题纸上
若式子 $\sqrt{x-2}$ 在实数范围内有意义,则 $x$ 的取值范围是
计算 $\sqrt{2} \cdot \sqrt{3}$ 的结果是
若 $\sqrt{x-9}$ 在实数范围内有意义,则实数 $x$ 的取值范围是
计算 $(\sqrt{11}-1)(\sqrt{11}+1)$ 的结果为
在函数 $y=\frac{\sqrt{x-3}}{x+2}$ 中,自变量 $x$ 的取值范围是
若代数式 $\frac{3}{\sqrt{x-1}}$ 在实数范围内有意义,则 $x$ 的取值范围为
计算:$\sqrt{12}-\sqrt{8} \cdot \sqrt{6}=$
在函数 $y=\frac{1}{\sqrt{3+x}}+\frac{1}{x+2}$ 中,自变量 $x$ 的取值范围是
解答题 (共 4 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
(1)先化简,再求值:$(x+1)^2-2(x+1)$ ,其中 $x=2 \sqrt{2}$ .
(2)解方程:$\frac{x-2}{x-4}-2=\frac{x}{x-4}$ .
计算:$|1-\sqrt{3}|+24^{\frac{1}{2}}+\frac{1}{2+\sqrt{3}}-(1-\sqrt{3})^0$
计算:$\sqrt{18}-\sqrt{12} \times \sqrt{\frac{3}{2}}$ .
(1)计算:$\sqrt{2} \times \sqrt{50}-(1-\sqrt{3})^0$ ;
(2)化简:$\left(\frac{3}{a-2}+1\right) \div \frac{a+1}{a^2-4}$ .