单选题 (共 8 题 ),每题只有一个选项正确
设集合 $A=\{0,1,2\}, B=|x|-3 < x \leqslant 2\}$, 则 $A \cap B=$
$\text{A.}$ $\{x \mid-2 \leqslant x \leqslant 2\}$
$\text{B.}$ $|x| 0 \leqslant x < 2\}$
$\text{C.}$ $\{0,1,2\}$
$\text{D.}$ $\{0,1\}$
已知复数 $z$ 满足 $(1-\mathrm{i}) z=3+\mathrm{i}(\mathrm{i}$ 是虚数单位), 则 $z=$
$\text{A.}$ $-1+2 \mathrm{i}$
$\text{B.}$ $-1-2 \mathrm{i}$
$\text{C.}$ $1-2 \mathrm{i}$
$\text{D.}$ $1+2 i$
已知双曲线 $C: x^2-\frac{y^2}{8}=1$, 其一条渐近线被圆 $(x-\sqrt{3})^2+y^2=3$ 截得弦长为
$\text{A.}$ $\frac{\sqrt{3}}{3}$
$\text{B.}$ $1$
$\text{C.}$ $\frac{2 \sqrt{3}}{3}$
$\text{D.}$ $2$
已知随机变量 $X$ 服从正态分布 $N\left(2, \sigma^2\right)$, 且 $P(X>3)=\frac{1}{6}$, 则 $P(X>1)=$
$\text{A.}$ $\frac{1}{6}$
$\text{B.}$ $\frac{1}{3}$
$\text{C.}$ $\frac{2}{3}$
$\text{D.}$ $\frac{5}{6}$
设 $\alpha, \beta$ 是两个不同的平面, $a, b$ 是两条不同的直线, 下列说法正确的是
$\text{A.}$ 若 $a \perp \alpha, b \perp \beta, a \perp b$, 则 $\alpha \perp \beta$
$\text{B.}$ 若 $a \perp \alpha, b \subset \beta, a \perp b$, 则 $\alpha \perp \beta$
$\text{C.}$ 若 $a \perp \alpha, b \perp \beta, a / / b$, 则 $\alpha \perp \beta$
$\text{D.}$ 若 $a \perp \alpha, a \perp b, \alpha \cap \beta=b$, 则 $\alpha \perp \beta$
某校对高三男生进行体能抽测, 每人测试三个项目, 1000 米为必测项目, 再从“引体向上, 仰卧起坐, 立定跳远” 中随机抽取两项进行测试, 则某班参加测试的 5 位男生测试项目恰好 相同的概率为
$\text{A.}$ $\frac{1}{243}$
$\text{B.}$ $\frac{1}{81}$
$\text{C.}$ $\frac{1}{27}$
$\text{D.}$ $\frac{1}{9}$
已知函数 $f(x)$ 的图象如图所示, 则该函数的解析式可 能是
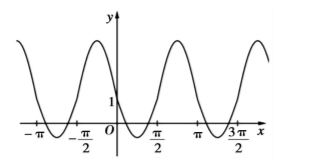
$\text{A.}$ $f(x)=|\sin x|+|\cos x|-2 \sin 2 x$
$\text{B.}$ $f(x)=|\sin x|-|\cos x|+2 \sin 2 x$
$\text{C.}$ $f(x)=|\sin x|-|\cos x|+2 \cos 2 x$
$\text{D.}$ $f(x)=|\sin x|+|\cos x|+2 \cos 2 x$
已知 $x_1=\log _5 2, x_2+\ln x_2=0,3^{-x_3}=\log _2 x_3$, 则
$\text{A.}$ $x_1 < x_2 < x_3$
$\text{B.}$ $x_2 < x_1 < x_3$
$\text{C.}$ $x_1 < x_3 < x_2$
$\text{D.}$ $x_2 < x_3 < x_1$
多选题 (共 4 题 ),每题有多个选项正确
关于平面向量 $a, b, c$, 下列说法不正确的是
$\text{A.}$ 若 $a \cdot c=b \cdot c$, 则 $a=b$
$\text{B.}$ $(a+b) \cdot c=a \cdot c+b \cdot c$
$\text{C.}$ 若 $a^2=b^2$, 则 $a \cdot c=b \cdot c$
$\text{D.}$ $(a \cdot b) c=(b \cdot c) a$
作为世界经济增长的重要引擎, 中国经济充满韧性活力, 备受世界瞩目. 当前, 新冠疫情 延宕反复, 全球通胀攀升, 美联储激进加息冲击全球, 世界经济下行压力明显增大. 在此背景下, 中国经济稳住了自身发展势头, 不断向世界经济输送宝贵增长动能, 续写世界经 济发展史上的中国奇迹. 中共二十大报告为中国的末来擘画了发展蓝图, 让全球经济界 人士继续看好中国经济光明前景. 根据世界银行最新公布的数据, 下列说法正确的是
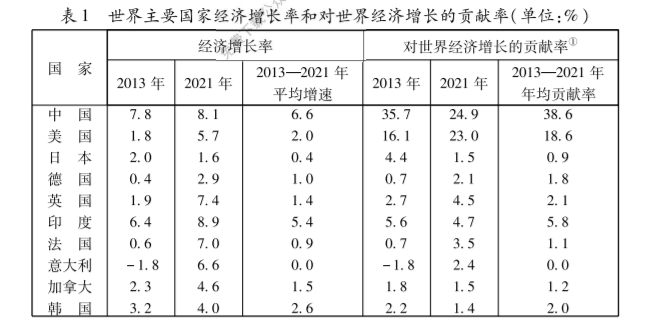
注: ①根据 2015 年为基期的国内生产总值计算. 资料来源: 世界银行 WDI 数据库.
$\text{A.}$ 2013-2021 年, 我国经济平均增速 6.6\%, 居世界主要经济体前列
$\text{B.}$ 2013-2021 年, 我国对世界经济增长的年均贡献率达到 $38.6 \%$, 超过表中其他国家年 均贡献率的总和, 是推动世界经济增长的第一动力
$\text{C.}$ 2021 年,我国的经济增长率位居世界第一
$\text{D.}$ 表中“2021 年世界主要国家经济增长率”这组数据的 75 百分位数是 $7.4 \%$
已知函数 $f(x)=\cos (\omega x+\varphi)\left(\omega>0,-\frac{\pi}{2} < \varphi < \frac{\pi}{2}\right)$, 将 $y=f(x)$ 的图象上所有点向右平移 $\frac{\pi}{3}$ 个单位长度, 然后横坐标伸长为原来的 2 倍, 纵坐标不变, 得到函数 $y=g(x)$ 的图象. 若 $g(x)$ 为奇函数,且最小正周期为 $\pi$, 则下列说法正确的是
$\text{A.}$ 函数 $f(x)$ 的图象关于点 $\left(\frac{\pi}{6}, 0\right)$ 中心对称
$\text{B.}$ 函数 $f(x)$ 在区间 $\left(0, \frac{\pi}{4}\right)$ 上单调递减
$\text{C.}$ 不等式 $g(x) \geqslant \frac{1}{2}$ 的解集为 $\left[k \pi-\frac{5 \pi}{12}, k \pi-\frac{\pi}{12}\right](k \in \mathrm{Z})$
$\text{D.}$ 方程 $f\left(\frac{x}{2}\right)=g(x)$ 在 $(0, \pi)$ 上有 2 个解
球冠是指球面被平面所截得的一部分曲面,截得的圆叫做球冠 的底,垂直于截面的直径被截得的一段叫做球冠的高. 小明撑 伞站在太阳下,撑开的伞面可以近似看作一个球冠. 已知该球 冠的底半径为 $60 \mathrm{~cm}$, 高为 $20 \mathrm{~cm}$. 假设地面是平面, 太阳光线是 平行光束, 下列说法正确的是
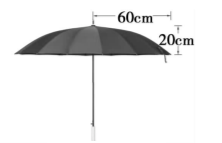
$\text{A.}$ 若伞柄垂直于地面, 太阳光线与地面所成角为 $\frac{\pi}{4}$, 则伞在地面的影子是圆
$\text{B.}$ 若伞柄垂直于地面, 太阳光线与地面所成角为 $\frac{\pi}{6}$, 则仝在地面的影子是椭圆
$\text{C.}$ 若伞柄与太阳光线平行, 太阳光线与地面所成角为 $\frac{\pi}{3}$, 则央在地面的影子为椭圆, 且该 椭圆离心率为 $\frac{1}{2}$
$\text{D.}$ 若太阳光线与地面所成角为 $\frac{\pi}{6}$, 则小明调整伞柄位置, 伞在地面的影子可以形成椭圆, 且椭圆长轴长的最大值为 $240 \mathrm{~cm}$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
$\left(\frac{2}{x}-x\right)^6$ 的展开式中 $x^2$ 的系数为.
已知数列 $\left\{a_n\right\}$ 中: $a_1=2, a_{n+1}=\left\{\begin{array}{l}a_n-1, n \text { 为奇数, } \\ 2 a_n+2, n \text { 为偶数, }\end{array}\right.$ 则 $\left\{a_n\right\}$ 的前 8 项和为
如图是我国古代测量粮食的容器 “升”, 其形状是正四棱台,“升” 装满后用手指或筷子沿升口刮平, 这叫“平升”, 若该“升”内粮食的高度为 “平升”的一半时, 粮食的体积约为 “平升”时体积的 $\frac{1}{4}$, 则该“升”升口边长与升底边长的比值为

若函数 $f(x)$ 的定义域为 $(0,+\infty)$, 且 $f(x)+f(y)=f(x y), f\left(a_n\right)=n+f(n)$, 则 $\sum_{i=1}^n f\left(\frac{a_i}{i}\right)=$
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
正项数列 $\left\{a_n \mid\right.$ 的前 $n$ 项和 $S_n$ 满足 $6 S_n=a_n^2+3 a_n+2$, 且 $a_1>1$.
(1) 求数列 $\left\{a_n\right\}$ 的通项公式;
(2) 设数列 $\left\{b_n \mid\right.$ 满足 $a_n\left(3^{b_n}-1\right)=3, T_n$ 为数列 $\left\{b_n\right\}$ 的前 $n$ 项和, 求 $3^{T_{100}}$.
已知 $\triangle A B C$ 的内角 $A, B, C$ 的对边分别为 $a, b, c, b=\sqrt{3}, a < c$, 且 $\sin \left(\frac{\pi}{3}-A\right) \cos \left(\frac{\pi}{6}+A\right)=\frac{1}{4}$.
(1) 求 $A$ 的大小;
(2) 若 $a \sin A+c \sin C=4 \sqrt{3} \sin B$, 求 $\triangle A B C$ 的面积.
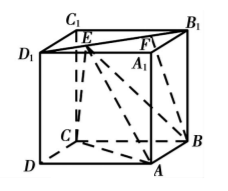
如图, 正方体 $A B C D-A_1 B_1 C_1 D_1$ 的棱长为 $1, E, F$ 是线段 $B_1 D_1$ 上的两个动点.
(1) 若 $B F / /$ 平面 $A C E$, 求 $E F$ 的长度;
(2) 若 $\overrightarrow{D_1 E}=\frac{1}{4} \overrightarrow{D_1 B_1}$, 求直线 $B E$ 与平面 $A C E$ 所成角的正弦值.
有研究显示, 人体内某部位的直径约 $10 \mathrm{~mm}$ 的结节约有 $0.2 \%$ 的可能性会在 1 年内发展为 恶性肿瘤. 某医院引进一台检测设备, 可以通过无创的血液检测, 估计患者体内直径约 $10 \mathrm{~mm}$ 的结节是否会在 1 年内发展为恶性肿瘤, 若检测结果为阳性, 则提示该结节会在 1 年内发展为恶性肿瘤, 若检测结果为阴性,则提示该结节不会在 1 年内发展为恶性肿瘤. 这种检测的准确率为 $85 \%$, 即一个会在 1 年内发展为恶性肿瘤的患者有 $85 \%$ 的可能性被 检出阳性,一个不会在 1 年内发展为恶性肿瘤的患者有 $85 \%$ 的可能性被检出阴性. 患者 甲被检查出体内长了一个直径约 $10 \mathrm{~mm}$ 的结节,他做了该项无创血液检测.
(1) 求患者甲检查结果为阴性的概率;
(2)若患者甲的检查结果为阴性, 求他的这个结节在 1 年内发展为恶性肿瘤的概率 (结果 保留 5 位小数);
(3) 医院为每位参加该项检查的患者缴纳 200 元保险费, 对于检测结果为阴性, 但在 1 年 内发展为恶性肿瘤的患者, 保险公司赔付该患者 20 万元, 若每年参加该项检查的患者 有 1000 人, 请估计保险公司每年在这个项目上的收益.
已知抛物线 $C: y^2=2 p x$, 点 $A(1,2)$ 在 $C$ 上, $A$ 关于动点 $T(t, 0)(t < 3)$ 的对称点记为 $M$, 过 $M$ 的直线 $l$ 与 $C$ 交于 $P\left(x_1, y_1\right), Q\left(x_2, y_2\right), M$ 为 $P, Q$ 的中点.
(1) 当直线 $l$ 过坐标原点 $O$ 时, 求 $\triangle A P Q$ 外接圆的标准方程;
(2) 求 $\triangle A P Q$ 面积的最大值.
已知函数 $f(x)=\ln (1+a x)-x-\frac{1}{a}, g(x)=x-\mathrm{e}^x$.
(1) 若不等式 $f(x) \leqslant \frac{1}{a}-2$ 恒成立, 求 $a$ 的取值范围;
(2) 若 $a=1$ 时, 存在 4 个不同实数 $x_1, x_2, x_3, x_4$, 满足 $f\left(x_1\right)=f\left(x_2\right)=g\left(x_3\right)=g\left(x_4\right)$, 证明: $\left|x_2-x_1\right|=\left|x_4-x_3\right|$.