单选题 (共 12 题 ),每题只有一个选项正确
复数 $z$ 满足 $1+z \mathrm{i}+z \mathrm{i}^2=|1-\sqrt{3} \mathrm{i}|$, 则 $z=$
$\text{A.}$ $1+\mathrm{i}$
$\text{B.}$ $\frac{1}{2}+\frac{1}{2} \mathrm{i}$
$\text{C.}$ $-\frac{1}{2}-\frac{1}{2} \mathrm{i}$
$\text{D.}$ $-\frac{1}{2}+\frac{1}{2} \mathrm{i}$
若集合 $M=\left\{x \mid 2^x>1\right\}, N=\left\{x \mid \log _3 x \leqslant 1\right\}$, 则 $M \cup N=$
$\text{A.}$ $\{x \mid 2 < x \leqslant 3\}$
$\text{B.}$ $\{x \mid x>0\}$
$\text{C.}$ $\{x \mid 0 < x < 2$ 或 $x>2\}$
$\text{D.}$ $\mathbf{R}$
已知 $S_n$ 是数列 $\left\{a_n\right\}$ 的前 $n$ 项和, 则 “ $a_n>0$ ” 是 “ $\left\{S_n\right\}$ 是递增数列” 的
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 充要条件
$\text{D.}$ 既不充分也不必要条件
某同学掷骰子 5 次, 分别记录每次骰子出现的点数, 根据 5 次的统计结果, 可以判断一定 没有出现点数 6 的是
$\text{A.}$ 中位数是 3 , 众数是 2
$\text{B.}$ 平均数是 3 , 中位数是 2
$\text{C.}$ 方差是 $2.1$, 平均数是 2
$\text{D.}$ 平均数是 3 , 众数是 2
.已知 $\sin \left(\alpha+\frac{\pi}{6}\right)-\cos \alpha=\frac{1}{2}$, 则 $\sin \left(2 \alpha+\frac{\pi}{6}\right)=$
$\text{A.}$ $-\frac{1}{2}$
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ $-\frac{3}{4}$
$\text{D.}$ $\frac{3}{4}$
已知圆台上底面半径为 1 , 下底面半径为 3 , 球与圆台的两个底面利侧面均相切, 则该圆 台的侧面积'球的表面积之比为
$\text{A.}$ $\frac{13}{6}$
$\text{B.}$ $\frac{4}{3} \sqrt{3}$
$\text{C.}$ $\frac{13}{12}$
$\text{D.}$ $\frac{4}{3}$
已知函数 $f(x)$ 及其导函数 $f^{\prime}(x)$ 的定义域均为 $\mathbf{R}$, 记 $g(x)=f(1+x)-x$, 若 $f^{\prime}(x)$ 为奇 函数, $g(x)$ 为偶函数, 则 $f^{\prime}(2023)=$
$\text{A.}$ 2021
$\text{B.}$ 2022
$\text{C.}$ 2023
$\text{D.}$ 2024
已知椭圆 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>b>0)$, 直线 $l$ 过坐标原点并交椭圆于 $P, Q$ 两点 $(P$ 在第一象
限), 点 $A$ 是 $x$ 轴正半轴上一点, 其横坐标是点 $P$ 横坐标的 2 倍, 直线 $Q A$ 交椭圆于点 $B$, 若直线 $B P$ 椧好是以 $P Q$ 为直径的圆的切线,则椭圆的㐫心率为
$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ $\frac{\sqrt{2}}{2}$
$\text{C.}$ $\frac{\sqrt{3}}{3}$
$\text{D.}$ $\frac{\sqrt{6}}{3}$
在正方体 $A B C D-A_1 B_1 C_1 D_1$ 中, $M, N, P$ 分别是面 $A B_1$, 面 $B_1 D_1$, 面 $D A_1$ 的中心, 则下列 结论正确的是

$\text{A.}$ $N P / / D C_1$
$\text{B.}$ $M N / /$ 平面 $A C P$
$\text{C.}$ $D_1 C \perp$ 平面 $M N P$
$\text{D.}$ $P M$ 与 $B C_1$ 所成的角是 $60^{\circ}$
将函数 $f(x)=\sin (2 x+\varphi)\left(|\varphi| < \frac{\pi}{2}\right)$ 的图像向左平移 $\frac{\pi}{4}$ 个单位得到函数 $g(x)$ 的图像, 若 $g(x)$ 的图像与 $f(x)$ 的图像关于 $y$ 轴对称, 则下列说法正确的有
$\text{A.}$ $\varphi=\frac{\pi}{4}$
$\text{B.}$ $\varphi=-\frac{\pi}{1}$
$\text{C.}$ $g(x)$ 的对称轴过 $f(x)$ 的对称中心
$\text{D.}$ $\forall m \in\left[-\frac{\pi}{4}, \frac{\pi}{8}\right], \exists n \in\left[-\frac{\pi}{4}, \frac{\pi}{8}\right]$,使得 $f(m)=g(n)$
设数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$, 且 $n S_n=(n+1) S_n+(n-1) n(n+1)\left(n \geqslant 2, n \in \mathbf{N}^*\right)$, 若 $S_1=-50$, 则下列结论正确的有
$\text{A.}$ $a_5>0$
$\text{B.}$ 当 $n=4$ 时, $S_n$ 取得最小值
$\text{C.}$ 当 $S_n>0$ 时, $n$ 的最小值为 7
$\text{D.}$ 当 $n=5$ 时, $\frac{S_n}{a_n}$ 取得最小值
已知函数 $f(x)$ 及其导函数 $f^{\prime}(x)$ 的定义域均为 $\mathbf{R}$, 若 $f^{\prime}(x)-f(x)=\dfrac{x-\sin x}{\mathrm{e}^x}, f(0)=1$, 则下列结论正确的是
$\text{A.}$ $f(1)>\mathrm{e}$
$\text{B.}$ $f^{\prime}\left(\frac{\pi}{2}\right) < f\left(\frac{\pi}{2}\right)$
$\text{C.}$ 方程 $f^{\prime}(x)=f(x)+\frac{1}{2 \mathrm{e}^2}$ 有两个解
$\text{D.}$ $f(x)$在$(0, \dfrac{\pi}{2})$ 上单调递增
填空题 (共 4 题 ),请把答案直接填写在答题纸上
二项式 $\left(1-\frac{1}{x}\right)(1+x)^6$ 展开式中 $x^3$ 的系数为
已知非零向量 $\boldsymbol{a}, \boldsymbol{b}$ 满足 $|\boldsymbol{b}|=2|\boldsymbol{a}+\boldsymbol{b}|,(\boldsymbol{a}+\boldsymbol{b}) \perp \boldsymbol{a}$, 则 $\boldsymbol{a}, \boldsymbol{b}$ 的夹角大小是
若关于 $x$ 的不等式 $(\ln x)^2-a x \ln x>0$ 有且只有一个整数解, 则实数 $a$ 的取值范围为
已知双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的左、右焦点分别为 $F_1$ 和 $F_2, O$ 为坐标原点, 过 $F_2$ 作渐近线 $y=\frac{b}{a} x$ 的垂线, 垂足为 $P$, 若 $\angle F_1 P O=\frac{\pi}{6}$, 则双曲线的离心率为 ; 又过点 $P$ 作双曲线的切线交另一条渐近线于点 $Q$, 且 $\triangle O P Q$ 的面积 $S_{\triangle O P Q}$ $=2 \sqrt{3}$, 则该双曲线的方程为
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知数列 $\left\{\ln a_n\right\}$ 是等差数列, 记 $S_n$ 为 $\left\{a_n\right\}$ 的前 $n$ 项和, $\left\{S_n+a_1\right\}$ 是等比数列, $a_1=1$.
(1) 求 $a_n$;
(2) 记 $b_n=\log _2 a_{2 n-1}+\log _2 a_{2 n}$, 求数列 $\left\{(-1)^n \cdot b_n{ }^2\right\}$ 的前 10 项和.
在 $\triangle A B C$ 中, 角 $A 、 B 、 C$ 所对的边分别为 $a 、 b 、 c$, 已知 $a 、 b 、 c$ 成等比数列, 且 $\cos (A-C)$ $+\cos B=\frac{3}{2}$
(1)求角 $A 、 B 、 C$;
(2) 若 $b=2$, 延长 $B C$ 至 $D$, 使 $\triangle A B D$ 的面积为 $\frac{3 \sqrt{3}}{2}$, 求 $\sin \angle C A D$.
党的二十大的胜利召开为我们建设社会主义现代化国家指引了前进的方向. 为讴歌中 华民族实现伟大复兴的奋斗历程, 增进高中学生对党的二十大的理解, 某校组织开展党 的二十大知识竞赛活动, 以班级为单位参加比赛, 最终甲、乙两班进行到了最后决赛, 决 赛采取五局三胜制, 约定先胜三局者贏得比赛. 已知每局比赛中必决出胜负, 每一局若 甲班先答题, 则甲获胜的概率为 $\frac{2}{3}$, 若乙班先答题, 则甲获胜的概率为 $\frac{1}{2}$, 每一局输的一 方在接下来的一局中先答题, 第一局由乙班先答题.
(1)求比赛一共进行了四局并且甲班最终赢得比赛的概率;
(2) 若规定每一局比赛中胜者得 2 分, 负者得 0 分, 记 $X$ 为比赛结束时甲班的总得分, 求 随机变量 $X$ 的分布列和数学期望.
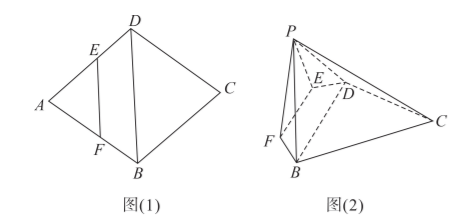
如图 (1), 菱形 $A B C D$ 中, $\angle A B C=120^{\circ}$, 动点 $E, F$ 分别在边 $A D, A B$ 上(不含端点), 且 $\overrightarrow{E F}=\lambda \overrightarrow{D B}(0 < \lambda < 1)$, 沿 $E F$ 将 $\triangle A E F$ 向上折起得到 $\triangle P E F$, 使得平面 $P E F \perp$ 平面 $B C D E F$, 如图 (2) 所示.
(1) 当 $\lambda$ 为何值时, $B F \perp P D$;
(2) 若直线 $P C$ 与平面 $B C D E F$ 所成角的正切值为 $\frac{1}{3}$, 求平面 $P E F$ 和平面 $P B D$ 夹角的 大小.
已知抛物线 $C: y^2=2 p x(p>0)$ 的准线与 $x$ 轴的交点为 $H$, 直线过抛物线 $C$ 的焦点 $F$ 且
与 $C$ 交于 $A, B$ 两点, $\triangle H A B$ 的面积的最小值为 4 .
(1) 求抛物线 $C$ 的方程;
(2) 若过点 $Q\left(\frac{17}{4}, 1\right)$ 的动直线 $l$ 交 $C$ 于 $M, N$ 两点, 试问抛物线 $C$ 上是否存在定点 $E$, 使得 对任意的直线 $l$, 都有 $E M \perp E N$, 若存在, 求出点 $E$ 的坐标; 若不存在, 则说明理由.
已知函数 $f(x)=\mathrm{e}^x-x+\mathrm{e}^3 a$, 其中 $-\frac{6}{5} \leqslant a < \frac{3}{\mathrm{e}^3}-1$, 函数 $f(x)$ 在 $(0,+\infty)$ 上的零点为 $x_0$, 函数 $g(x)=\left\{\begin{array}{l}x+a-\frac{x-a}{\mathrm{e}^x}, 0 \leqslant x \leqslant x_0, \\ (1-x) \ln x-a(x+1), x>x_0 .\end{array}\right.$
(1)证明:
(1) $3 < x_0 < 4$;
(2) 函数 $g(x)$ 有两个零点;
(2) 设 $g(x)$ 的两个零点为 $x_1, x_2\left(x_1 < x_2\right)$, 证明: $\frac{\mathrm{e}^{x_2}-x_2}{\mathrm{e}^{x_1}-x_1}>\mathrm{e}^{\frac{x_1+x_2}{2}}$.
(参考数据: $\mathrm{e} \approx 2.72, \mathrm{e}^2 \approx 7.39, \mathrm{e}^3 \approx 20.09, \ln 2 \approx 0.69, \ln 3 \approx 1.1$ )