单选题 (共 4 题 ),每题只有一个选项正确
下列函数是偶函数的是
$\text{A.}$ $y=\sin x$
$\text{B.}$ $y=\cos x$
$\text{C.}$ $y=x^3$
$\text{D.}$ $y=2^x$
根据下图判断, 下列选项错误的是
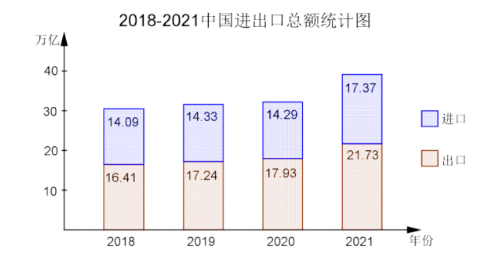
$\text{A.}$ 从 2018 年开始, 2021 的进出口总额增长率最大
$\text{B.}$ 从 2018 年开始, 进出口总额逐年增大
$\text{C.}$ 从 2018 年开始, 进口总额逐年增大
$\text{D.}$ 从 2018 年开始, 2020 的进出口总额增长率最小
如图所示, 正方体 $A B C D-A_1 B_1 C_1 D_1$ 中, $P$ 是 $A_1 C_1$ 上的 动点, 则下列直线中, 始终与直线 $B P$ 异面的是

$\text{A.}$ $D D_1$
$\text{B.}$ $A C$
$\text{C.}$ $A D_1$
$\text{D.}$ $B_1 C$
数列 $\left\{a_n\right\}$ 的各项均为实数, $S_n$ 为其前 $n$ 项和, 对任意 $k>2022(k \in \mathbf{N})$ 都有 $\left|S_k\right|>\left|S_{k+1}\right|$, 则下列说法正确的是
$\text{A.}$ $a_1 、 a_3 、 a_5 、 \cdots 、 a_{2 n-1}$ 为等差数列, $a_2 、 a_4 、 a_6 、 \cdots 、 a_{2 n}$ 为等比数列
$\text{B.}$ $a_1 、 a_3 、 a_5 、 \cdots 、 a_{2 n-1}$ 为等比数列, $a_2 、 a_4 、 a_6 、 \cdots 、 a_{2 n}$ 为等差数列
$\text{C.}$ $a_1 、 a_2 、 a_3 、 \cdots 、 a_{2022}$ 为等差数列, $a_{2023} 、 a_{2024} 、 \cdots 、 a_n$ 为等比数列
$\text{D.}$ $a_1 、 a_2 、 a_3 、 \cdots 、 a_{2022}$ 为等比数列, $a_{2023} 、 a_{2024} 、 \cdots 、 a_n$ 为等差数列
填空题 (共 12 题 ),请把答案直接填写在答题纸上
已知集合 $A=\{1,2\}, B=\{1, a\}$, 且 $A=B$, 则 $a=$
已知向量 $\vec{a}=(3,4), \vec{b}=(1,2)$, 则 $\vec{a}-2 \vec{b}=$
若不等式 $|x-1| \leq 2$, 则 $x$ 的取值范围是
已知圆 $C$ 的一般方程为 $x^2+2 x+y^2=0$, 则圆 $C$ 的半径为
已知事件 $A$ 发生的概率为 $P(A)=0.5$, 则它的对立事件 $P(\bar{A})=$
已知正实数 $a 、 b$ 满足 $a+4 b=1$, 则 $a b$ 的最大值为
某校抽取 100 名学生测身高, 其中身高最大值为 $186 \mathrm{~cm}$, 最小值 $154 \mathrm{~cm}$, 根据身高数据 绘制频率组距分布直方图, 组距为 5 , 且第一组下限为 $153.5 \mathrm{~cm}$, 则组数为
设 $(1-2 x)^4=a_0+a_1 x+a_2 x^2+a_3 x^3+a_4 x^4$, 则 $a_0+a_4=$
已知函数 $f(x)=2^{-x}+1$, 且 $g(x)=\left\{\begin{array}{l}\log _2(x+1), x \geq 0 \\ f(-x), x < 0\end{array}\right.$, 则方程 $g(x)=2$ 的解为
已知有 4 名男生, 6 名女生, 从 10 人中任选 3 人, 则恰有 1 名男生 2 名女生的概率为
设 $z_1 、 z_2 \in \mathbf{C}$ 且 $z_1=\mathrm{i} \cdot \overline{z_2}$, 满足 $\left|z_1-1\right|=1$, 则 $\left|z_1-z_2\right|$ 的取值范围为
设 $\overrightarrow{O A} 、 \overrightarrow{O B} 、 \overrightarrow{O C}$ 为空间中三组单位向量, 且 $\overrightarrow{O A} \perp \overrightarrow{O B}, \overrightarrow{O A} \perp \overrightarrow{O C}, \overrightarrow{O B}$ 与 $\overrightarrow{O C}$ 夹角 为 $60^{\circ}, P$ 为空间任意一点, 且 $|\overrightarrow{O P}|=1$, 满足 $|\overrightarrow{O P} \cdot \overrightarrow{O C}| \leq|\overrightarrow{O P} \cdot \overrightarrow{O B}| \leq|\overrightarrow{O P} \cdot \overrightarrow{O A}|$, 则 $|\overrightarrow{O P} \cdot \overrightarrow{O C}|$ 最大值为
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
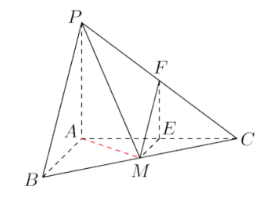
已知 $P A \perp$ 平面 $A B C, A B \perp A C, P A=A B=3, A C=4, M$ 为 $B C$ 中点, 过点 $M$ S分别作平行于平面 $P A B$ 的直线交 $A C 、 P C$ 于点 $E 、 F$.
(1) 求直线 $P M$ 与平面 $A B C$ 所成的角;
(2) 证明: 平面 $M E F / /$ 平面 $P A B$, 并求直线 $M E$ 到平面 $P A B$ 的距离.
在 $\triangle A B C$ 中, 角 $A 、 B 、 C$ 对应边为 $a 、 b 、 c$, 其中 $b=2$.
(1) 若 $A+C=\frac{2 \pi}{3}$, 且 $a=2 c$, 求边长 $c$ 的值;
(2) 若 $A-C=\frac{\pi}{12}, a=\sqrt{2} c \sin A$, 求 $S_{\triangle A B C}$.
为了节能环保, 节约材料、定义建筑物的 “体形系数” 为 $S=\frac{F_0}{V_0}$, 其中 $F_0$ 为建筑物暴 露在空气中的面积 (单位: 平方米), $V_0$ 为建筑物的体积 (单位: 立方米)
(1) 若有一圆柱形建筑物的底面半径为 $R$, 高度为 $H$, 求该建筑物的 “体形系数”;
(结果用含 $R 、 H$ 的代数式表示)
(2) 定义建筑物的 “形状因子” 为 $f=\frac{L^2}{A}$, 其中 $A$ 为底面面积, $L$ 为建筑底面周长,
又定义 $T$ 为总建筑面积, 即为每层建筑面积总和(每层建筑面积为每一层的底面面积). 现有一垂直于底面的宿舍, 已知该宿舍的层高为 3 米, 有 $n$ 层, 其 “形状因子” $f=18$, 总建筑面积为 $T=10000$ 平方米, 试求当该宿舍的层数 $n$ 为多少时, “体形系数” $S$ 最小.
椭圆 $\Gamma: \frac{x^2}{m^2}+\frac{y^2}{3}=1(m>0, m \neq \sqrt{3})$
(1) 若 $m=2$, 求椭圆 $\Gamma$ 的离心率;
(2) 设 $A_1 、 A_2$ 为椭圆 $\Gamma$ 的左右顶点, 椭圆 $\Gamma$ 上一点 $E$ 的纵坐标为 1 , 且 $\overrightarrow{E A_1} \cdot \overrightarrow{E A_2}=-2$, 求 $m$ 的值;
(3) 过椭圆 $\Gamma$ 上一点 $P$ 作斜率为 $\sqrt{3}$ 的直线, 与双曲线 $\frac{y^2}{5 m^2}-\frac{x^2}{5}=1$ 有一个公共点, 求 $m$ 的取值范围.
设函数 $f(x)=a x^3-(a+1) x^2+x, g(x)=k x+m$, 其中 $a \geq 0, k 、 m \in \mathbf{R}$, 若对任意 $x \in[0,1]$ 均有 $f(x) \leq g(x)$, 则称函数 $y=g(x)$ 是函数 $y=f(x)$ 的 “控制函数” , 且对所有 的函数 $y=g(x)$ 取最小值定义为 $\bar{f}(x)$.
(1) 若 $a=2, g(x)=x$, 试问 $y=g(x)$ 是否为函数 $y=f(x)$ 的 “控制函数”;
(2) 若 $a=0$, 使得直线 $y=h(x)$ 是曲线 $y=f(x)$ 在 $x=\frac{1}{4}$ 处的切线.
证明: 函数 $y=h(x)$ 为函数 $y=f(x)$ 的 “控制函数” , 并求 $\bar{f}\left(\frac{1}{4}\right)$ 的值;
(3) 若曲线 $y=f(x)$ 在 $x=x_0, x_0 \in(0,1)$ 处的切线过点 $(1,0)$, 且 $c \in[0,1]$.
证明:当且仅当 $c=x_0$ 或 $c=1$ 时, $\bar{f}(c)=f(c)$.