单选题 (共 10 题 ),每题只有一个选项正确
设集合 $A=\{1,2\}, B=\{2,4,6\}$, 则 $A \cup B=$
$\text{A.}$ $\{2\}$
$\text{B.}$ $\{1,2\}$
$\text{C.}$ $\{2,4,6\}$
$\text{D.}$ $\{1,2,4,6\}$
已知 $a, b \in \mathbf{R}, a+3 \mathrm{i}=(b+\mathrm{i}) \mathrm{i}(\mathrm{i}$ 为虚数单位), 则
$\text{A.}$ $a=1, b=-3$
$\text{B.}$ $a=-1, b=3$
$\text{C.}$ $a=-1, b=-3$
$\text{D.}$ $a=1, b=3$
若实数 $x, y$ 满足约束条件$\left\{\begin{array}{l}
x-2 \geq 0 \\
2 x+y-7 \leq 0 \\
x-y-2 \leq 0
\end{array}\right.$ 则 $ z=3 x+4 y$ 最大值是
$\text{A.}$ 20
$\text{B.}$ 18
$\text{C.}$ 13
$\text{D.}$ 6
设 $x \in \mathbf{R}$, 则“ $\sin x=1$ ”是“ $\cos x=0$ ”的
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 充分必要条件
$\text{D.}$ 既不充分也不必要条件
某几何体的三视图如图所示 (单位: $\mathrm{cm}$ ), 则该几何体的体积 (单位: $\mathrm{cm}^3$ ) 是
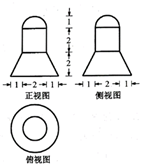
$\text{A.}$ $22 \pi$
$\text{B.}$ $8 \pi$
$\text{C.}$ $\frac{22}{3} \pi$
$\text{D.}$ $\frac{16}{3} \pi$
为了得到函数 $y=2 \sin 3 x$ 的图象, 只要把函数 $y=2 \sin \left(3 x+\frac{\pi}{5}\right)$ 图象上所有的点
$\text{A.}$ 向左平移 $\frac{\pi}{5}$ 个单位长度
$\text{B.}$ 向右平移 $\frac{\pi}{5}$ 个单位长度
$\text{C.}$ 向左平移 $\frac{\pi}{15}$ 个单位长度
$\text{D.}$ 向右平移 $\frac{\pi}{15}$ 个单位长度
. 已知 $2^a=5, \log _8 3=b$, 则 $4^{a-3 b}=$
$\text{A.}$ $25$
$\text{B.}$ $5$
$\text{C.}$ $\frac{25}{9}$
$\text{D.}$ $\frac{5}{3}$
如图, 已知正三棱柱 $A B C-A_1 B_1 C_1, A C=A A_1, E, F$ 分别是棱 $B C, A_1 C_1$ 上的点. 记 $E F$ 与 $A A_1$ 所成的角为 $\alpha, E F$ 与平面 $A B C$ 所成的角为 $\beta$, 二面角 $F-B C-A$ 的平面 角为 $\gamma$, 则
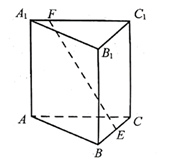
$\text{A.}$ $\alpha \leq \beta \leq \gamma$
$\text{B.}$ $\beta \leq \alpha \leq \gamma$
$\text{C.}$ $\beta \leq \gamma \leq \alpha$
$\text{D.}$ $\alpha \leq \gamma \leq \beta$
已知 $a, b \in \mathbf{R}$, 若对任意 $x \in \mathbf{R}, a|x-b|+|x-4|-|2 x-5| \geq 0$, 则
$\text{A.}$ $a \leq 1, b \geq 3$
$\text{B.}$ $a \leq 1, b \leq 3$
$\text{C.}$ $a \geq 1, b \geq 3$
$\text{D.}$ $a \geq 1, b \leq 3$
已知数列 $\left\{a_n\right\}$ 满足 $a_1=1, a_{n+1}=a_n-\frac{1}{3} a_n^2\left(n \in \mathbf{N}^*\right)$, 则
$\text{A.}$ $2 < 100 a_{100} < \frac{5}{2}$
$\text{B.}$ $\frac{5}{2} < 100 a_{100} < 3$
$\text{C.}$ $3 < 100 a_{100} < \frac{7}{2}$
$\text{D.}$ $\frac{7}{2} < 100 a_{100} < 4$
填空题 (共 7 题 ),请把答案直接填写在答题纸上
我国南宋著名数学家秦九韶, 发现了从三角形三边求面积的公式, 他把这种方法称为“三斜 求积", 它填补了我国传统数学的一个空白. 如果把这个方法写成公式, 就是 $S=\sqrt{\frac{1}{4}\left[c^2 a^2-\left(\frac{c^2+a^2-b^2}{2}\right)^2\right]}$, 其中 $a, b, c$ 是三角形的三边, $S$ 是三角形的面积. 设 某三角形的三边 $a=\sqrt{2}, b=\sqrt{3}, c=2$, 则该三角形的面积 $S=$
已知多项式 $(x+2)(x-1)^4=a_0+a_1 x+a_2 x^2+a_3 x^3+a_4 x^4+a_5 x^5$, 则 $a_2=$ $a_1+a_2+a_3+a_4+a_5=$
若 $3 \sin \alpha-\sin \beta=\sqrt{10}, \alpha+\beta=\frac{\pi}{2}$, 则 $\sin \alpha=$ , $\cos 2 \beta=$
已知函数 $f(x)=\left\{\begin{array}{l}-x^2+2, x \leq 1, \\ x+\frac{1}{x}-1, x>1,\end{array}\right.$ 则 $f\left(f\left(\frac{1}{2}\right)\right)=$ ; 若当 $x \in[a, b]$ 时, $1 \leq f(x) \leq 3$, 则 $b-a$ 的最大值是
现有 7 张卡片, 分别写上数字 $1,2,2,3,4,5,6$. 从这 7 张卡片中随机抽取 3 张, 记所抽取卡片上数字的最小值为 $\xi$, 则 $P(\xi=2)=$ , $E(\xi)=$
已知双曲线 $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的左焦点为 $F$, 过 $F$ 且斜率为 $\frac{b}{4 a}$ 的直线交双曲线于点 $A\left(x_1, y_1\right)$, 交双曲线的渐近线于点 $B\left(x_2, y_2\right)$ 且 $x_1 < 0 < x_2$. 若 $|F B|=3|F A|$, 则双曲线 的离心率是
设点 $P$ 在单位圆的内接正八边形 $A_1 A_2 \mathrm{~L} A_8$ 的边 $A_1 A_2$ 上, 则 $\overrightarrow{P A}_1^2+{\overrightarrow{P A_2}}^2+\cdots+\overrightarrow{P A}_8^2$ 的 取值范围是
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
在 $\triangle A B C$ 中, 角 $A, B, C$ 所对的边分别为 $a, b, c$. 已知 $4 a=\sqrt{5} c, \cos C=\frac{3}{5}$.
(1) 求 $\sin A$ 的值;
(2) 若 $b=11$, 求 $\triangle A B C$ 的面积.
如图, 已知 $A B C D$ 和 $C D E F$ 都是直角梯形, $A B / / D C, D C / / E F, A B=5$, $D C=3, E F=1, \angle B A D=\angle C D E=60^{\circ}$, 二面角 $F-D C-B$ 的平面角为 $60^{\circ}$. 设 $M, N$ 分别为 $A E, B C$ 的中点.
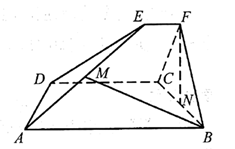
(1) 证明: $F N \perp A D$;
(2) 求直线 $B M$ 与平面 $A D E$ 所成角的正弦值.
已知等差数列 $\left\{a_n\right\}$ 的首项 $a_1=-1$, 公差 $d>1$. 记 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n\left(n \in \mathbf{N}^*\right)$.
(1) 若 $S_4-2 a_2 a_3+6=0$, 求 $S_n$;
(2) 若对于每个 $n \in \mathbf{N}^*$, 存在实数 $c_n$, 使 $a_n+c_n, a_{n+1}+4 c_n, a_{n+2}+15 c_n$ 成等比数列, 求 $d$ 的取值范围.
如图, 已知椭圆 $\frac{x^2}{12}+y^2=1$. 设 $A, B$ 是椭圆上异于 $P(0,1)$ 的两点, 且点 $Q\left(0, \frac{1}{2}\right)$ 在线段 $A B$ 上, 直线 $P A, P B$ 分别交直线 $y=-\frac{1}{2} x+3$ 于 $C, D$ 两点.
(1) 求点 $P$ 到椭圆上点的距离的最大值;
(2) 求 $|C D|$ 的最小值.

设函数 $f(x)=\frac{e}{2 x}+\ln x(x>0)$.
(1) 求 $f(x)$ 的单调区间;
(2) 已知 $a, b \in \mathbf{R}$, 曲线 $y=f(x)$ 上不同的三点 $\left(x_1, f\left(x_1\right)\right),\left(x_2, f\left(x_2\right)\right),\left(x_3, f\left(x_3\right)\right)$ 处的切线 都经过点 $(a, b)$. 证明:
(i) 若 $a>e$, 则 $0 < b-f(a) < \frac{1}{2}\left(\frac{a}{e}-1\right)$;
(ii) 若 $0 < a < e, x_1 < x_2 < x_3$, 则 $\frac{2}{e}+\frac{e-a}{6 e^2} < \frac{1}{x_1}+\frac{1}{x_3} < \frac{2}{a}-\frac{e-a}{6 e^2}$.
(注: $e=2.71828 \cdots$ 是自然对数的底数)