单选题 (共 12 题 ),每题只有一个选项正确
设集合 $M=\{1,3,5,7,9\}, N=\{x \mid 2 x>9\}$, 则 $M \cap N=()$
$\text{A.}$ $\{7,9\}$
$\text{B.}$ $\{5,7,9\}$
$\text{C.}$ $\{3,5,7,9\}$
$\text{D.}$ $\{1,3,5,7,9\}$
若复数 $z$ 满足 $\mathrm{i} \cdot z=1+4 \sqrt{3} \mathrm{i}$, 则 $|z|=(\quad)$
$\text{A.}$ 1
$\text{B.}$ 5
$\text{C.}$ 7
$\text{D.}$ 25
已知命题 $P: \forall x \in(0,+\infty), 3 x \leq x^3$, 则 $\neg p$ 是
$\text{A.}$ $\exists x_0 \in(-\infty, 0], 3 x_0 \leq x_0^3$
$\text{B.}$ $\exists x_0 \in(0,+\infty), 3 x_0>x_0{ }^3$
$\text{C.}$ $\forall x \in(-\infty, 0], 3 x \leq x^3$
$\text{D.}$ $\forall x \in(0,+\infty), 3 x>x^3$
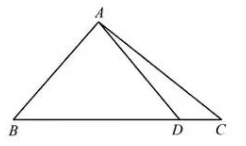
如图, 在 $\triangle A B C$ 中, $\overrightarrow{B D}=4 \overrightarrow{D C}$, 则 $\overrightarrow{A D}=(\quad)$
$\text{A.}$ $\frac{1}{5} \overrightarrow{A B}+\frac{4}{5} \overrightarrow{A C}$
$\text{B.}$ $\frac{4}{5} \overrightarrow{A B}+\frac{1}{5} \overrightarrow{A C}$
$\text{C.}$ $\frac{1}{6} \overrightarrow{A B}+\frac{5}{6} \overrightarrow{A C}$
$\text{D.}$ $\frac{5}{6} \overrightarrow{A B}+\frac{1}{6} \overrightarrow{A C}$
函数 $f(x)=\left(\frac{2^x-1}{2^x+1}\right) \sin x$ 在 $\left[-\frac{3 \pi}{2}, \frac{3 \pi}{2}\right]$ 上的图象的大致形状是
$\text{A.}$ 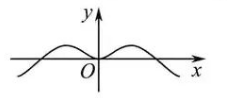 $\text{B.}$
$\text{B.}$ 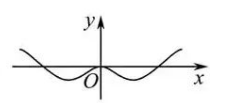 $\text{C.}$
$\text{C.}$ 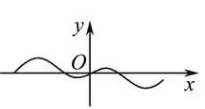 $\text{D.}$
$\text{D.}$ 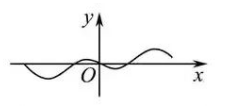
斐波那契数列 $\left\{F_n\right\}$ 因数学家莱昂纳多·斐波那契 (LeonardodaFibonaci) 以兔子繁殖为例而引 入, 故又称为 “兔子数列”. 因 $n$ 趋向于无穷大时, $\frac{F_n}{F_{n+1}}$ 无限趋近于黄金分割数, 也被称为 黄金分割数列. 在数学上, 斐波那契数列由以下递推方法定义: 数列 $\left\{F_n\right\}$ 满足 $F_1=F_2=1$, $F_{n+2}=F_{n+1}+F_n$, 若从该数列前 10 项中随机抽取 1 项, 则抽取项是奇数的概率为
$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ $\frac{3}{10}$
$\text{C.}$ $\frac{2}{3}$
$\text{D.}$ $\frac{7}{10}$
某建筑物如图所示, 底部为 $\mathrm{A}$, 顶部为 $B$, 点 $C, D$ 与点 $\mathrm{A}$ 在同一水平线上, 且 $|C D|=l$, 用高为 $h$ 的测角工具在 $C, D$ 位置测得建筑物顶部 $B$ 在 $C_1$ 和 $D_1$处的仰角分别为 $\alpha, \beta$. 其中 $C_1, D_1$ 和 $\mathrm{A}_1$ 在同一条水平线上, $A_1$ 在 $A B$ 上, 则该建筑物的高 $A B=(\quad)$
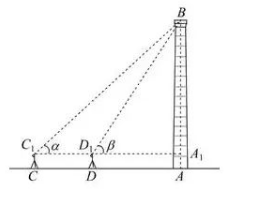
$\text{A.}$ $\frac{l \sin \alpha \cos \beta}{\sin (\beta-\alpha)}+h$
$\text{B.}$ $\frac{l \cos \alpha \cos \beta}{\sin (\beta-\alpha)}+h$
$\text{C.}$ $\frac{l \cos \alpha \sin \beta}{\sin (\beta-\alpha)}+h$
$\text{D.}$ $\frac{l \sin \alpha \sin \beta}{\sin (\beta-\alpha)}+h$
已知直线 $k x-y+2=0$ 与椭圆 $\frac{x^2}{9}+\frac{y^2}{m}=1$ 恒有公共点, 则实数 $m$ 的取值范围
$\text{A.}$ $(4,9]$
$\text{B.}$ $[4,+\infty)$
$\text{C.}$ $[4,9) \cup(9,+\infty)$
$\text{D.}$ $(9,+\infty)$
执行如图所示的程序框图, 输出的结果为 258 , 则判断框内可填入的条 件为
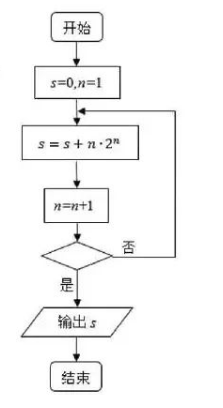
$\text{A.}$ $n \geq 4$ ?
$\text{B.}$ $n \geq 5$ ?
$\text{C.}$ $n \geq 6$ ?
$\text{D.}$ $n \geq 7$ ?
对于函数 $f(x)=\left\{\begin{array}{l}\sin x, \sin x \geq \cos x \\ \cos x, \sin x < \cos x\end{array}\right.$, 给出下列四个命题:
(1) 该函数的值域是 $[-1,1]$;
(2) 当且仅当 $x=2 k \pi+\frac{\pi}{2}(k \in Z)$ 时, 该函数取得最大值 1 ;
(3)该函数的最小正周期为 $2 \pi$;
(4) 当且仅当 $2 k \pi+\pi < x < 2 k \pi+\frac{3 \pi}{2}(k \in \mathrm{Z})$ 时, $f(x) < 0$; 其中所有正确命题个数有
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
设定义 $R$ 在上的函数 $y=f(x)$, 满足任意 $x \in R$, 都有 $f(x+4)=f(x)$, 且 $x \in(0,4]$ 时, $x f^{\prime}(x)>f(x)$, 则 $f(2021), \frac{f(2022)}{2}, \frac{f(2023)}{3}$ 的大小关系是
$\text{A.}$ $f(2021) < \frac{f(2022)}{2} < \frac{f(2023)}{3}$
$\text{B.}$ $\frac{f(2022)}{2} < f(2021) < \frac{f(2023)}{3}$
$\text{C.}$ $\frac{f(2023)}{3} < \frac{f(2022)}{2} < f(2021)$
$\text{D.}$ $\frac{f(2023)}{3} < f(2021) < \frac{f(2022)}{2}$
已知函数 $f(x)=\frac{1}{3} x^3+\frac{1}{2} b x^2+c x+d$ 有两个极值点 $x_1, x_2$, 若 $f\left(x_1\right)=x_1 < x_2$, 则关于 $x$ 的方程 $[f(x)]^2+b f(x)+c=0$ 的不同实根个数为
$\text{A.}$ 2
$\text{B.}$ 3
$\text{C.}$ 4
$\text{D.}$ 5
填空题 (共 4 题 ),请把答案直接填写在答题纸上
已知等差数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$, 若 $a_2+a_6=10$, 则 $S_7=$
中心在原点的双曲线, 其渐近线方程是 $y=\pm \sqrt{2} x$, 且过点 $(2, \sqrt{2})$, 则双曲线的标准方程 为
已知三棱锥 $P-A B C$ 的各顶点都在同一球面上, 且 $P C \perp$ 平面 $A B C$, 若该棱雉的体积为 2 , $A B=2, B C=\sqrt{3}, \angle A B C=30^{\circ}$, 则此球的表面积等于
已知向量 $\vec{a}$ 与 $\vec{b}$ 夹角为锐角, 且 $|\vec{a}|=|\vec{b}|=2$, 任意 $\lambda \in R,|\vec{a}-\lambda \cdot \vec{b}|$ 的最小值为 $\sqrt{3}$, 若向量 $\vec{c}$ 满足 $(\vec{c}-\vec{a}) \cdot(\vec{c}-\vec{b})=0$, 则 $\mid \vec{q}$ 的取值范围为
解答题 (共 7 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
在 $\triangle A B C$ 中, 设角 $\mathrm{A}, B, C$ 的对边分别为 $a, b, c$. 已知向量 $\vec{m}=(\sqrt{3} \cos A, \sin A), \vec{n}=(1,-1)$, 且 $\vec{m} / / \vec{n}$.
(1) 求角 $\mathrm{A}$ 的大小;
(2) 若 $a=2 \sqrt{6}, a \sin B-c \sin A=0$, 求 $\triangle A B C$ 的面积.
自 2019 年 1 月 1 日起, 对个人所得税起征点和税率进行调整。调整如 下: 纳税人的工资、薪金所得, 以每月全部收入额减去 5000 元后的余额为应纳税所得额。 依照个人所得税税率表, 调整前后的计算方法如表:
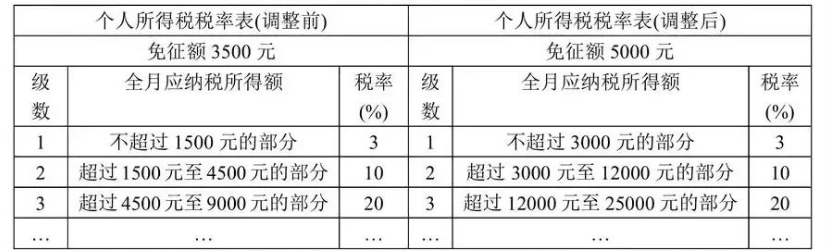
(1) 假如李先生某月的工资、薪金等所得税前收入总和不高于 8000 元, 记 $x$ 表示总收入, $y$ 表示应纳的税, 试分别求出调整前和调整后 $y$ 关于 $x$ 的函数表达式;
(2) 某税务部门在李先生所在公司利用分层抽样方法抽取某月 100 个不同层次员工的税前 收入, 并制成下面的频数分布表:

先从收入在 $[3000,5000)$ 及 $[5000,7000)$ 的人群中按分层抽样抽取 7 人, 再从中选 2 人作为新纳税法知识宣讲员, 求选中的 2 人收入都在 $[3000,5000)$ 的概率;
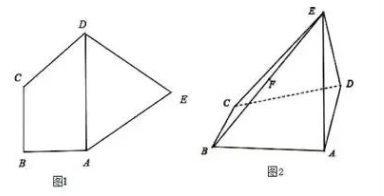
在平面五边形 $A B C D E$ 中 (如图 1), $A B C D$ 是梯形, $A D / / B C$, $A D=2 B C=2 \sqrt{2}, \quad A B=\sqrt{2}, \quad \angle A B C=90^{\circ}$,
$\triangle A D E$ 是等边三角形. 现将 $\triangle A D E$ 沿 $A D$ 折 起, 连接 $E B, E C$ 得四棱雉 $E-A B C D$ (如 图 2), 且 $E C=2 \sqrt{2}$.
(1) 求证: 平面 $E A D \perp$ 平面 $A B C D$;
(2) 若 $F$ 是棱 $E B$ 的中点, 求 $C F$ 与平面 $A B C D$ 所成角的正切值.
已知抛物线 $C: y^2=2 p x(p>0)$ 上一点 $M(3, t)$ 到准线的距离为 4 , 焦点 为 $\mathrm{F}$, 坐标原点为 $O$, 直线 $l$ 与抛物线 $C$ 交于 $\mathrm{A}, \mathrm{B}$ 两点 (与 $O$ 点均不重合).
(1) 求抛物线 $C$ 方程;
(2) 若以 $A B$ 为直径的圆过原点 $O$, 求 $\triangle A B F$ 与 $\triangle B O F$ 的面积之和的最小值.
已知函数 $f(x)=x \ln x-x-\frac{a x^2}{2}+1(a \in \mathbf{R})$.
(1)当 $a=1$ 时, 求 $f(x)$ 在 $(1, f(1))$ 处的切线方程;
(2) 若函数 $f(x)$ 有两个不同的极值点 $x_1, x_2$. 求证: $x_1 x_2 < \frac{1}{a^2}$.
在平面直角坐标系 $x O y$ 中, 曲线 $\mathrm{C}$ 满足参数方程为 $\left\{\begin{array}{l}x=2 \cos \alpha \\ y=2 \sin \alpha\end{array}\right.$ ~$\alpha$ 为 参数, $\alpha \in[-\pi, 0]$ ). 以坐标原点为极点, $x$ 轴的非负半轴为极轴建立极坐标系, 直线 $l$ 的 极坐标方程为 $\rho \cos \theta+\rho \sin \theta-m=0$.
(1) 求曲线 $\mathrm{C}$ 和直线 $l$ 的直角坐标方程;
(2) 若直线 $l$ 与曲线 $\mathrm{C}$ 交于 $\mathrm{A}, \mathrm{B}$ 两点, 且 $\overrightarrow{O A} \cdot \overrightarrow{O B}=2$, 求实数 $m$ 的值.
已知函数 $f(x)=|x-1|-|x+2|$.
(1) 求不等式 $f(x) < 2 x$ 的解集;
(2) 记函数 $f(x)$ 的最大值为 $M$. 若正实数 $a, b, c$ 满足 $a+b+4 c=\frac{1}{3} M$, 求证: $\frac{1}{a}+\frac{1}{b}+\frac{1}{c} \geq 16$.