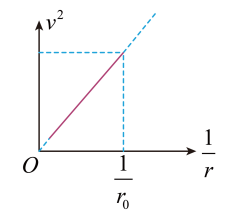
宇航员驾驶宇宙飞船绕质量分布均匀的一星球做匀速圆周运动, 测得飞船线速度大小的二次方与轨道半径的倒数的关系图如图中实线所示, 该图线 (直线) 的斜率为 $k$, 图中 $r_0$ (该星球的半径) 为已知量。引力常量为 $G$, 下列说法正确的是

A. 该星球的密度为 $\frac{3 G}{4 \pi k r_0^3}$
B. 该星球的自转周期为 $\sqrt{\frac{r_0^2}{k}}$
C. 该星球表面的重力加速度大小为 $\frac{k}{r_0^2}$
D. 该星球的第一宇宙速度为 $\sqrt{\frac{k}{r_0}}$