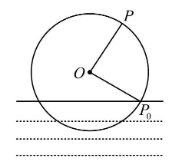
一半径为4.8m的水轮如图所示,水轮圆心$O$距离水面2.4m,已知水轮每60s逆时针转动一圈,如果当水轮上点$P$从水中浮现时(图中点$P_0$)开始计时,则( ).

A. 点$P$离水面的距离$d$(单位:m)与时间$t$(单位:s)的函数解析式为$d=4.8\sin\left(\dfrac{\pi}{30}t-\dfrac{\pi}{6}\right)-2.4$
B. 点$P$第一次到达最高点需要10s
C. 在水轮转动的一圈内,点$P$离水面的高度不低于4.8m共有10s时间
D. 当水轮转动50s时,点$P$在水面下方,距离水面2.4m