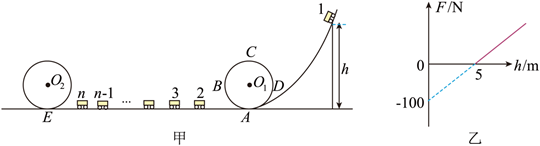
某过山车模型轨道如图甲所示, $O_1 、 O_2$ 为半径分别为 $r_1 、 r_2$ 的圆形轨道, 它们在最低点分别与两侧平直轨 道顺滑连接, 不计轨道各部分摩擦及空气阻力, 小车的长度 $l$ 远小于圆形轨道半径 $r$, 各游戏车分别编号为 $1 、 2 、 3 \cdots \mathrm{n}$, 质量均为 $m$, 圆形轨道 $A B C D$ 最高点 $C$ 处有一压力传感器。让小车 1 从右侧轨道不同高度 处从静止滑下, 压力传感器的示数随高度 $h$ 变化, 作出 $F-h$ 关系如图乙所示。
(1) 根据图乙信息, 分析小车 1 质量 $m$ 及圆形轨道 $O_1$ 半径 $r_1$;
(2) 在水平轨道 $A E$ 区间(不包含 $A$ 和 $E$ 两处), 自由停放有编号为 $2 、 3 \cdots \mathrm{n}$ 的小车, 让 1 号车从 $h=5 \mathrm{~m}$ 高处由静止滑下达到水平轨道后依次与各小车发生碰撞, 各车两端均装有挂钩, 碰后便连接不再脱钩, 求 在作用过程中, 第 $n$ 辆车受到合力的冲量及合力对它做的功。
(3) 轨道 $O_2$ 半径为 $r_2=2.5 \mathrm{~m}$, 每辆车长度为 $L$, 且 $n L>2 \pi r_2$, 要使它们都能安全通过轨道 $O_2$, 则 1 车至少从多大高度滑下?
(1) 根据图乙信息, 分析小车 1 质量 $m$ 及圆形轨道 $O_1$ 半径 $r_1$;
(2) 在水平轨道 $A E$ 区间(不包含 $A$ 和 $E$ 两处), 自由停放有编号为 $2 、 3 \cdots \mathrm{n}$ 的小车, 让 1 号车从 $h=5 \mathrm{~m}$ 高处由静止滑下达到水平轨道后依次与各小车发生碰撞, 各车两端均装有挂钩, 碰后便连接不再脱钩, 求 在作用过程中, 第 $n$ 辆车受到合力的冲量及合力对它做的功。
(3) 轨道 $O_2$ 半径为 $r_2=2.5 \mathrm{~m}$, 每辆车长度为 $L$, 且 $n L>2 \pi r_2$, 要使它们都能安全通过轨道 $O_2$, 则 1 车至少从多大高度滑下?
