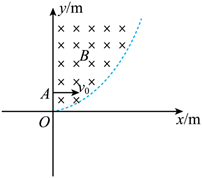
如图所示, $x O y$ 坐标系的第一象限内分布着垂直纸面向里的有界匀强磁场 $B=1 \mathrm{~T}$, 磁场的右边界是满足 $y=\frac{1}{2} x^2$ (单位: $\mathrm{m}$ ) 的抛物线的一部分, 现有一质量 $m=1 \times 10^{-6} \mathrm{~kg}$, 电荷量 $q=2 \times 10^{-4} \mathrm{C}$ 的带正电粒子 (重力不计)从 $y$ 轴上的 $A$ 点 $(0,0.5 \mathrm{~m})$ 沿 $x$ 轴正向以 $v$ 射入, 恰好不从磁场右边界射出, 则

A. 粒子在磁场中做逆时针圆周运动
B. 粒子到达磁场边界的位置坐标为 $(\sqrt{2} \mathrm{~m}, 1 \mathrm{~m})$
C. 粒子在磁场中运动的速率为 $2 \times 10^2 \mathrm{~m} / \mathrm{s}$
D. 粒子从 $A$ 点到磁场右边界的运动时间为 $\frac{\pi}{6} \times 10^{-2} \mathrm{~s}$